题目内容
函数y=logx+1(2x+1)的单调递减区间为 .
考点:复合函数的单调性
专题:函数的性质及应用
分析:对x+1分类讨论,利用对数函数、一次函数、复合函数的单调性即可得出.
解答:
解:当x+1>1,即x>0时,由y=2x+1单调递增,可得:函数y=logx+1(2x+1)单调递增,不符合题意,舍去.
当0<x+1<1,即-1<x<0时,由函数y=2x+1(>0)单调递增,因此函数y=logx+1(2x+1)单调递减,满足题意.
∴函数y=logx+1(2x+1)的单调递减区间是(-1,0).
故答案为:(-1,0).
当0<x+1<1,即-1<x<0时,由函数y=2x+1(>0)单调递增,因此函数y=logx+1(2x+1)单调递减,满足题意.
∴函数y=logx+1(2x+1)的单调递减区间是(-1,0).
故答案为:(-1,0).
点评:本题考查了对数函数、一次函数、复合函数的单调性,考查了分类讨论思想方法,考查了推理能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知集合A到B的映射f:x→y=
,则集合A中元素3在B中所对应的元素是( )
| 12 |
| x+1 |
| A、1 | B、2 | C、3 | D、4 |
下列关系中正确的是( )
A、log76<ln
| ||
B、log3π<ln
| ||
C、ln
| ||
D、ln
|
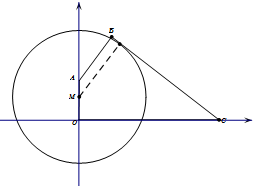 已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO=
已知四边形OABC中,OA⊥OC,AB⊥BC,且OA=6,OC=17,tan∠BCO= 如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积.
如图是一个几何体的三视图(单位:cm),计算这个几何体的体积与表面积. 三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.
三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠ABC=90°,AB=BC=BB1=2,M,N分别是AB,A1C的中点.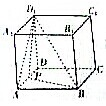 如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.
如图所示,在正方体ABCD-A1B1C1D1中,P是棱AD的中点,求二面角A-BD1-P的大小.