题目内容
如图程序框图是古代一数学家的算法程序框图，它输出的结果S代表（ ）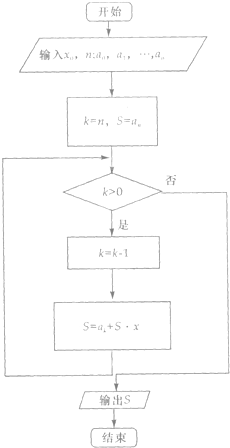
| A、一个数列的和 |
| B、一个n次多项式系数的和 |
| C、自变量取x．时，n次多项式函数的值 |
| D、自变量取x时，n个代数式的值 |
考点：程序框图
专题：算法和程序框图
分析：根据题意，模拟程序框图的运行过程，即可得出该程序运行输出的结果是什么．
解答：
解：模拟程序框图的运行过程，如下；
输入x，n，a0，a1，a2，…，an，
k=n，S=an，k＞0，是，k=n-1，S=an-1+S•x=an-1+anx；
k＞0，是，k=n-2，S=an-2+S•x=an-2+（an-1+anx）x=an-2+an-1x+anx2；
…；
k＞0，是，k=1，S=a1+S•x=a1+a2x+a3x2+…+anxn-1；
k＞0，是，k=0，S=a0+S•x=a0+a1x+a2x2+a3x3+…+anan；
k＞0，否，输出S=a0+S•x=a0+a1x+a2x2+a3x3+…+anan；
∴输出S是代表自变量取x时，n次多项式函数的值．
故选：C．
输入x，n，a0，a1，a2，…，an，
k=n，S=an，k＞0，是，k=n-1，S=an-1+S•x=an-1+anx；
k＞0，是，k=n-2，S=an-2+S•x=an-2+（an-1+anx）x=an-2+an-1x+anx2；
…；
k＞0，是，k=1，S=a1+S•x=a1+a2x+a3x2+…+anxn-1；
k＞0，是，k=0，S=a0+S•x=a0+a1x+a2x2+a3x3+…+anan；
k＞0，否，输出S=a0+S•x=a0+a1x+a2x2+a3x3+…+anan；
∴输出S是代表自变量取x时，n次多项式函数的值．
故选：C．
点评：本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
已知某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图如图所示，则甲、乙两人得分的中位数之和是已知A={x∈Z|-2＜x＜4}，B={x|
≥1}，则A∩（∁RB）的元素个数为（ ）
| 2 |
| x-1 |
| A、1 | B、2 | C、3 | D、4 |
与向量
=（-5，4）平行的向量是（ ）
| a |
| A、（-5k，4k） | ||||
B、（-
| ||||
| C、（-10，2） | ||||
| D、（5k，4k） |
若
＜
＜0，则下列结论不正确的是（ ）
| 1 |
| a |
| 1 |
| b |
A、
| ||||||
| B、a2＞b2 | ||||||
| C、a3＞b3 | ||||||
| D、|a|+|b|=|a+b| |
“a，b，c为实数，如果a=b，b=c，则a=c”．类比得到下列四个命题，其中假命题为（ ）
| A、a，b，c为空间三条不重合的直线，如果a⊥b，b⊥c，那么a⊥c |
| B、a，b，c为空间三条不重合的直线，如果a∥b，b∥c，那么a∥c |
| C、a，b，c为实数，如果a＞b，b＞c，那么a＞c |
| D、A，B，C为集合，如果A?B，B?C，那么A?C |
集合M={y|y=|cos2x|，x∈R}，集合N={x||
|＜1，i为虚数单位，x∈R}，则M∩N为（ ）
| x |
| i |
| A、（0，1） |
| B、[0，1） |
| C、（0，1] |
| D、[0，1] |
在不等式|x-1|+|x-4|≥3中，等号成立的充要条件是（ ）
| A、x≥4或x≤1 |
| B、1≤x≤4 |
| C、x=4或x=1 |
| D、x∈R |
点通过矩阵M1=
和M2=
的变换效果相当于另一变换是（ ）
|
|
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|