题目内容
16.已知f(x)=$\left\{\begin{array}{l}{{a}^{x}-a,x>1}\\{{x}^{2}+\frac{1}{2}ax-2,x≤1}\end{array}\right.$是(-$\frac{3}{8}$,+∞)上的增函数,那么a的取值范围是( )| A. | ($\frac{3}{2}$,2) | B. | (1,2] | C. | [$\frac{3}{2}$,2] | D. | (1,2) |
分析 根据分段函数在(-$\frac{3}{8}$,+∞)上是增函数,y1=ax-a,x>1必须是增函数,即a>1,(1,+∞)单调递增,那么y2=${x}^{2}+\frac{1}{2}ax-2,x≤1$,其对称轴x=$-\frac{a}{4}$,在[$-\frac{a}{4}$,1]必须是单调递增.结合单调递增的性质,y1≥y2可得结论.
解答 解:分段函数在(-$\frac{3}{8}$,+∞)上是增函数,y1=ax-a,x>1必须是增函数,即a>1,(1,+∞)单调递增,
那么y2=${x}^{2}+\frac{1}{2}ax-2,x≤1$,其对称轴x=$-\frac{a}{4}$,在[$-\frac{a}{4}$,1]必须是单调递增.
∴$-\frac{3}{8}≥-\frac{a}{4}$,解得:$a≥\frac{3}{2}$.
在(-$\frac{3}{8}$,+∞)上是增函数,那么y1的最小值要大于y2的最大值,即1$+\frac{1}{2}a-2≤0$,
解得:a≤2
∴a的取值范围是[$\frac{3}{2}$,2].
故选:C.
点评 本题考查了分段函数单调性的运用,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
6.向面积为S的平行四边形ABCD中任投一点M,则△MCD的面积小于$\frac{S}{3}$的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
11.给出下面四个命题(其中m,n,l为空间中不同的直线,α,β是空间中不同的平面)中正确的命题为( )
| A. | m∥n,n∥α⇒m∥α | B. | α⊥β,α∩β=m,l⊥m⇒l⊥β | ||
| C. | l⊥m,l⊥n,m?α,n?α⇒l⊥α | D. | m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β |
1.已知R是实数集,A={y|y=2x-1,x∈R},B={x|y=log2(1-x2)},则A∩B=( )
| A. | (-1,+∞) | B. | (-1,1) | C. | [-1,1) | D. | (1,+∞) |
5.要得到函数y=3cos2x的图象,只需将函数$y=3cos({2x+\frac{π}{3}})$的图象( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
16.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 无法确定 |
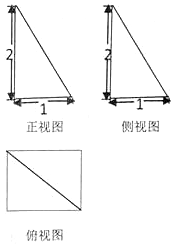 已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点.
已知四棱锥P-ABCD,PA⊥底面ABCD,其三视图如下,若M是PD的中点. 已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.
已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.