题目内容
8. 已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.
已知点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上.(1)分别求幂函数f(x),g(x)的解析式,并在同一直角坐标系中画出两个函数的图象;
(2)观察图象,并指出当x为何值时,有:①f(x)>g(x);②f(x)=g(x);③f(x)<g(x).
分析 (1)由点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上,可得函数的解析式,进而画出两个函数的图象;
(2)数形结合,可以得到①当x<0,或x>1时,f(x)>g(x);②当x=1时,f(x)=g(x);③当0<x<1时,f(x)<g(x).
解答 解:(1)设f(x)=xa,g(x)=xb,
由点$({\sqrt{2},2})$与点$({-2,-\frac{1}{2}})$分别在幂函数f(x),g(x)的图象上可得:
${\sqrt{2}}^{a}=2$,(-2)b=$-\frac{1}{2}$,
解得:a=2,b=-1,
故f(x)=x2,g(x)=x-1,
故在同一直角坐标系中画出两个函数的图象,如图所示: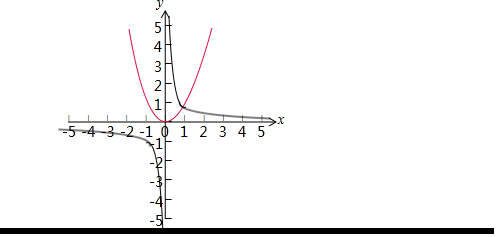
(2)由图可得:
①当x<0,或x>1时,f(x)>g(x);
②当x=1时,f(x)=g(x);
③当0<x<1时,f(x)<g(x).
点评 本题考查的知识点是幂函数的图象和性质,数形结合思想,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知f(x)=$\left\{\begin{array}{l}{{a}^{x}-a,x>1}\\{{x}^{2}+\frac{1}{2}ax-2,x≤1}\end{array}\right.$是(-$\frac{3}{8}$,+∞)上的增函数,那么a的取值范围是( )
| A. | ($\frac{3}{2}$,2) | B. | (1,2] | C. | [$\frac{3}{2}$,2] | D. | (1,2) |
3.已知sin(3π+α)=2sin$({\frac{3π}{2}+α})$,求下列各式的值:
(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α+sin 2α.
(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α+sin 2α.
13.已知集合M={第一象限角},N={锐角},P={小于90°角},则下列关系式中正确的是( )
| A. | M=N=P | B. | M?P=N | C. | M∩P=N | D. | N∩P=N |
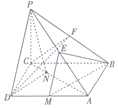 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.