题目内容
11.给出下面四个命题(其中m,n,l为空间中不同的直线,α,β是空间中不同的平面)中正确的命题为( )| A. | m∥n,n∥α⇒m∥α | B. | α⊥β,α∩β=m,l⊥m⇒l⊥β | ||
| C. | l⊥m,l⊥n,m?α,n?α⇒l⊥α | D. | m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β |
分析 对于A,若m∥n,n∥α,则m∥α或m?α,由此可判断A的正误;
对于B,由面面垂直的性质定理可判断B的正误;
对于C,由线面垂直的判定定理知判断C的正误;
对于D,由面面平行的判定定理可判断D的正误.
解答 解:对于A,m∥n,n∥α⇒m∥α或m?α,故A错误;
对于B,由面面垂直的性质定理知,若α⊥β,α∩β=m,l?α,l⊥m则l⊥β,若α⊥β,α∩β=m,l⊥m,但l?α,则l不一定垂直于β,故B错误;
对于C,由线面垂直的判定定理知:l⊥m,l⊥n,m?α,n?α,m∩n=P⇒l⊥α,C选项中缺少“m∩n=P”这个条件,故C错误;
对于D,m∩n=A,m∥α,m∥β,n∥α,n∥β⇒α∥β,这是面面平行的判定定理,故D正确;
综上所述,只有D正确,
故选:D.
点评 本题考查命题的真假判断与应用,着重考查空间线面、面面的位置关系及线面平行、面面平行与垂直的判断定理与性质定理的应用,考查空间想象能力,与逻辑思维能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知f(x)=$\left\{\begin{array}{l}{{a}^{x}-a,x>1}\\{{x}^{2}+\frac{1}{2}ax-2,x≤1}\end{array}\right.$是(-$\frac{3}{8}$,+∞)上的增函数,那么a的取值范围是( )
| A. | ($\frac{3}{2}$,2) | B. | (1,2] | C. | [$\frac{3}{2}$,2] | D. | (1,2) |
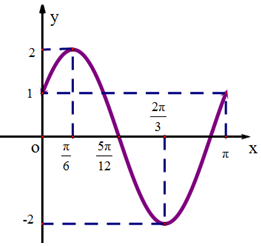 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.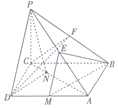 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.