题目内容
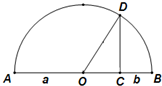如图所示，在⊙O上半圆中，AC=a，CB=b，CD⊥AB，请你利用CD≤OD写出一个含有a，b的不等式考点：基本不等式
专题：直线与圆
分析：如图所示，连接AD、DB．利用圆的性质可得∠ADB=90°．利用射影定理可得DC2=AC•CB，再利用DC≤OD=
，即可得出．
| a+b |
| 2 |
解答：
解：如图所示，
连接AD、DB．
∵AB是⊙O的直径，∴∠ADB=90°．
又∵DC⊥AB，
∴DC2=AC•CB，
∴DC=
．
∵AC+CB=a+b为⊙O的直径，
DC≤OD=
，
∴
≤
．
故答案为：
≤
．
连接AD、DB．∵AB是⊙O的直径，∴∠ADB=90°．
又∵DC⊥AB，
∴DC2=AC•CB，
∴DC=
| ab |
∵AC+CB=a+b为⊙O的直径，
DC≤OD=
| a+b |
| 2 |
∴
| ab |
| a+b |
| 2 |
故答案为：
| ab |
| a+b |
| 2 |
点评：本题考查了圆的性质、射影定理等基础知识，属于基础题．
练习册系列答案
相关题目
如图在等腰直角三角形ABC中，AB=AC=2，D、E是线段BC上的两点，且DE=若a∈R，则“a=3”是“（a+1）（a-3）=0”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
己知定义在R上的函数y=f（x）满足f（x）=f（4-x），且当x≠2时，其导函数f′（x）满足f′（x）＞
xf′（x），若a∈（2，3），则（ ）
| 1 |
| 2 |
| A、f（log2a）＜f（2a）＜f（2） |
| B、f（2a）＜f（2）＜f（log2a） |
| C、f（2a）＜f（log2a）＜f（2） |
| D、f（2）＜f（log2a）＜f（2a） |
下列命题中，真命题的是（ ）
| A、?x∈R，x2＞0 |
| B、?x∈R，-1＜sinx＜1 |
| C、?x0∈R，2x0＜0 |
| D、?x0∈R，tanx0=2 |