题目内容
二项式(ax+2)6的展开式的第二项的系数为12,则
x2dx= .
| ∫ | a -2 |
考点:定积分
专题:导数的综合应用
分析:利用二项式定理求出a的值,然后根据积分公式即可得到结论.
解答:
解:二项式(ax+2)6的展开式的第二项为
(ax)5•2=12a5x5,
则第二项的系数为12a5=12,解得a=1,
∴
x2dx=
x2dx=
x3
=3,
故答案为:3
| C | 1 6 |
则第二项的系数为12a5=12,解得a=1,
∴
| ∫ | a -2 |
| ∫ | 1 -2 |
| 1 |
| 3 |
| | | 1 -2 |
故答案为:3
点评:本题主要考查二项式定理以及的定积分的计算,要求熟练掌握相应的公式.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知集合M={x∈R|-3≤x≤1},N={x∈R|x+1<0},那么M∩N=( )
| A、{-1,0,1} |
| B、{-3,-2,-1} |
| C、{x|-1≤x≤1} |
| D、{x|-3≤x<-1} |
圆锥的底面半径是r,高是h,在这个圆锥内部有一个正方体.正方体的一个面在圆锥的底面上,与这个面相对的面的四个顶点在圆锥的侧面上,则此正方体的棱长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某正三棱锥的三视图如图所示,则该正三棱锥侧视图的面积为
某正三棱锥的三视图如图所示,则该正三棱锥侧视图的面积为
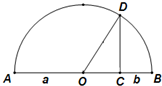 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式