题目内容
 如图在等腰直角三角形ABC中,AB=AC=2,D、E是线段BC上的两点,且DE=
如图在等腰直角三角形ABC中,AB=AC=2,D、E是线段BC上的两点,且DE=| 1 |
| 3 |
| AD |
| AE |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
=
,
=
,
=λ
,0≤λ≤
.利用平面向量基本定理表示出
,
.根据数量积的运算得到
•
=8λ2-
λ+
=8(λ-
)2+
.利用二次函数的性质即可求出
•
的取值范围.
| AB |
| a |
| AC |
| b |
| BD |
| BC |
| 2 |
| 3 |
| AD |
| AE |
| AD |
| AE |
| 16 |
| 3 |
| 8 |
| 3 |
| 1 |
| 3 |
| 16 |
| 9 |
| AD |
| AE |
解答:
解:设
=
,
=
,
=λ
,0≤λ≤
.
则
=
+λ(
-
).
∵DE=
BC,
∴
=(λ+
)
.
∴
=
+(λ+
)(
-
).
∴
•
=(
+λ(
-
))•(
+(λ+
)(
-
))
=((1-λ)
+λ
)((
-λ)
+(λ+
)
)
∵
⊥
,且|
|=|
|=2,
∴上式可化简为
•
=8λ2-
λ+
=8(λ-
)2+
.
∴当λ=
时,
•
取最小值为
.
当λ=0或
时,
•
取最大值为
.
∴
•
的取值范围是[
,
].
故答案为:[
,
].
| AB |
| a |
| AC |
| b |
| BD |
| BC |
| 2 |
| 3 |
则
| AD |
| a |
| b |
| a |
∵DE=
| 1 |
| 3 |
∴
| BE |
| 1 |
| 3 |
| BC |
∴
| AE |
| a |
| 1 |
| 3 |
| b |
| a |
∴
| AD |
| AE |
| a |
| b |
| a |
| a |
| 1 |
| 3 |
| b |
| a |
=((1-λ)
| a |
| b |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
∵
| a |
| b |
| a |
| b |
∴上式可化简为
| AD |
| AE |
| 16 |
| 3 |
| 8 |
| 3 |
=8(λ-
| 1 |
| 3 |
| 16 |
| 9 |
∴当λ=
| 1 |
| 3 |
| AD |
| AE |
| 16 |
| 9 |
当λ=0或
| 2 |
| 3 |
| AD |
| AE |
| 8 |
| 3 |
∴
| AD |
| AE |
| 16 |
| 9 |
| 8 |
| 3 |
故答案为:[
| 16 |
| 9 |
| 8 |
| 3 |
点评:本题考查平面向量基本定理,向量的数量积以及二次函数的性质等知识的综合应用,属于中档题.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、命题“若a>b,则2a>2b-1”的否命题为“若a>b,则2a≤2b-1” |
| B、命题“存在x∈R,使得x2+x+1<0”的否定是:“任意x∈R,都有x2+x+1>0” |
| C、若命题“非p”与命题“p或q”都是真命题,那么命题q一定是真命题 |
| D、命题“若a2+b2=0,则ab=0”的逆命题是真命题 |
已知集合M={x∈R|-3≤x≤1},N={x∈R|x+1<0},那么M∩N=( )
| A、{-1,0,1} |
| B、{-3,-2,-1} |
| C、{x|-1≤x≤1} |
| D、{x|-3≤x<-1} |
已知a,b∈(0,+∞),则“ab>2”是“log2a+log2b>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
一个几何体的三视图如图,则该几何体的体积为( )


| A、6π+4 |
| B、12π+4 |
| C、6π+12 |
| D、12π+12 |

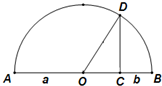 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式