题目内容
焦点为F的抛物线y2=4x上有三点A、B、C满足:①△ABC的重心是F;②|FA|、|FB|、|FC|成等差数列.则直线AC的方程是 .
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:利用△ABC的重心是F,可得y1+y2+y3=0,x1+x2+x3=3,|FA|、|FB|、|FC|成等差数列,可求B的坐标,进而可得直线AC的斜率,从而可得直线AC的方程.
解答:
解:设A、B、C三点的坐标分别为(x1,y1),(x2,y2),(x3,y3),
∵抛物线y2=4x的焦点F的坐标为F(1,0),△ABC的重心是F
∴
(x1+x2+x3)=1,y1+y2+y3=0,可得x1+x2+x3=3,
∵|FA|、|FB|、|FC|成等差数列,
∴2|FB|=|FA|+|FC|,
∴2(x2+1)=x1+1+x3+1,
∴2x2=x1+x3,
∴x2=1,
∴y2=±2,
∴y1+y3=±2,
∴kAC=
=
=±2,
设直线AC的方程是y=2x+b,代入y2=4x可得4x2+(4b-4)x+b2=0,
∴x1+x3=-b+1=2
∴b=-1,
同理直线AC的方程是y=-2x+b,代入y2=4x,可得b=-1,
∴直线AC的方程是2x±y-1=0.
故答案为:2x±y-1=0.
∵抛物线y2=4x的焦点F的坐标为F(1,0),△ABC的重心是F
∴
| 1 |
| 3 |
∵|FA|、|FB|、|FC|成等差数列,
∴2|FB|=|FA|+|FC|,
∴2(x2+1)=x1+1+x3+1,
∴2x2=x1+x3,
∴x2=1,
∴y2=±2,
∴y1+y3=±2,
∴kAC=
| y3-y1 |
| x3-x1 |
| 4 |
| y1+y3 |
设直线AC的方程是y=2x+b,代入y2=4x可得4x2+(4b-4)x+b2=0,
∴x1+x3=-b+1=2
∴b=-1,
同理直线AC的方程是y=-2x+b,代入y2=4x,可得b=-1,
∴直线AC的方程是2x±y-1=0.
故答案为:2x±y-1=0.
点评:本题考查抛物线方程,考查抛物线的定义,考查学生的计算能力,确定直线AC的斜率是关键.

练习册系列答案
相关题目
“α=
”是“cos2α=0”的( )
| π |
| 4 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不是充分条件也不是必要条件 |
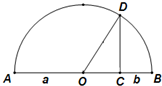 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式