题目内容
已知函数f(x)=sin
x,任取t∈R,记函数f(x)在区间[t,t+1]上的最大值为Mt,最小值为mt,记h(t)=Mt-mt.则关于函数h(t)有如下结论:
①函数h(t)为偶函数;
②函数h(t)的值域为[1-
,1];
③函数h(t)的周期为2;
④函数h(t)的单调增区间为[2k+
,2k+
],k∈Z.
其中正确的结论有 .(填上所有正确的结论序号)
| π |
| 2 |
①函数h(t)为偶函数;
②函数h(t)的值域为[1-
| ||
| 2 |
③函数h(t)的周期为2;
④函数h(t)的单调增区间为[2k+
| 1 |
| 2 |
| 3 |
| 2 |
其中正确的结论有
考点:命题的真假判断与应用,函数的值域,函数的单调性及单调区间,函数奇偶性的判断
专题:函数的性质及应用
分析:可先求出函数f(x)的最小正周期为4,由周期性得到h(t+4)=Mt-mt=h(t),说明h(t)是周期为4的函数,然后探索-2≤t≤2的函数f(x)的最值,以及h(t)的解析式,最后画出它的部分图象,通过图象观察分析得到性质,从而判断正确的结论.
解答:
解:∵f(x)=sin
的最小正周期为
=4,
∴Mt+4=Mt,mt+4=mt,
∴h(t+4)=Mt+4-mt+4=Mt-mt=h(t),
即h(t)是周期为4的函数,
∴对该函数的性质研究,只须探索t∈[-2,2]的性质即可.
画出函数f(x)=sin
的部分图象,如右图 ,
,
当-2≤t<-1.5,时,f(x)在区间[t,t+1]上的最小值为-1,最大值为f(t)=sin
,∴h(t)=1+sin
;
当-1.5≤t<-1时,f(x)在区间[t,t+1]上的最小值为-1,最大值为f(t+1)=sin
=cos
,∴h(t)=1+cos
;
当-1≤t<0时,f(x)在区间[t,t+1]上的最小值为f(t)=sin
,最大值为f(t+1)=sin
=cos
,∴h(t)=cos
-sin
;
当0≤t<
时,f(x)在区间[t,t+1]上的最小值为sin
,最大值为1,∴h(t)=1-sin
;
当
≤t<1时,f(x)在区间[t,t+1]上的最小值f(t+1)=sin
=cos
,最大值为1,∴h(t)=1-cos
;
当1≤t<2时,f(x)在区间[t,t+1]上的最小值为f(t+1)=sin
=cos
,最大值为f(t)=sin
,∴h(t)=sin
-cos
.
画出h(t)的部分图象,如右图,
综上可知,该函数没有奇偶性,
函数的值域为[1-
,
],函数的最小正周期为2,
函数的单调增区间为[2k+
,2k+
],k∈Z,
故①②错,③④正确.
故答案为:③④.
| πx |
| 2 |
| 2π | ||
|
∴Mt+4=Mt,mt+4=mt,
∴h(t+4)=Mt+4-mt+4=Mt-mt=h(t),
即h(t)是周期为4的函数,
∴对该函数的性质研究,只须探索t∈[-2,2]的性质即可.
画出函数f(x)=sin
| πx |
| 2 |
 ,
,当-2≤t<-1.5,时,f(x)在区间[t,t+1]上的最小值为-1,最大值为f(t)=sin
| πt |
| 2 |
| πt |
| 2 |
当-1.5≤t<-1时,f(x)在区间[t,t+1]上的最小值为-1,最大值为f(t+1)=sin
| πt+π |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
当-1≤t<0时,f(x)在区间[t,t+1]上的最小值为f(t)=sin
| πt |
| 2 |
| πt+π |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
当0≤t<
| 1 |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
当
| 1 |
| 2 |
| πt+π |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
当1≤t<2时,f(x)在区间[t,t+1]上的最小值为f(t+1)=sin
| πt+π |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
| πt |
| 2 |
画出h(t)的部分图象,如右图,

综上可知,该函数没有奇偶性,
函数的值域为[1-
| ||
| 2 |
| 2 |
函数的单调增区间为[2k+
| 1 |
| 2 |
| 3 |
| 2 |
故①②错,③④正确.
故答案为:③④.
点评:本题主要考查函数的周期性以及应用,根据周期性探索一个周期的情况,分别讨论每一个区间的情况:求出最值,写出函数式,最后通过图象得到有关性质,同时考查函数的最值和单调性、奇偶性,是一道难题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知一个几何体的三视图及有关数据如图所示,则该几何体的体积为( )


A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
设数列{an}为等差数列,若a1+a3+a13+a15=120,则a8=( )
| A、60 | B、30 | C、20 | D、15 |
已知集合A={x|-1<2x+1<5},集合B={x|y=lg(1-x2)},则( )
| A、A⊆B | B、B⊆A |
| C、A∪B=B | D、A∩B=A |
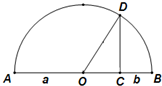 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式