题目内容
数列{an}的前n项和为Sn,且a1=3,an=2Sn-1+3n(n≥2),则该数列的通项公式为an= .
考点:等差数列的前n项和,数列递推式
专题:等差数列与等比数列
分析:由已知条件条件推导出数列{
}是以1为首项,
为公差的等差数列,由此能求出数列{an}的通项公式.
| an |
| 3n |
| 2 |
| 3 |
解答:
解:∵a1=3,an=2Sn-1+3n(n≥2),
∴an-1=2Sn-2+3n-1(n≥3),
相减得an-an-1=2an-1+2×3n-1,
∴an=3an-1+2×3n-1,
∴
=
+
,
∴数列{
}是以1为首项,
为公差的等差数列,
∴
=1+(n-1)×
,
∴an=(2n+1)•3n-1.
故答案为:(2n+1)•3n-1.
∴an-1=2Sn-2+3n-1(n≥3),
相减得an-an-1=2an-1+2×3n-1,
∴an=3an-1+2×3n-1,
∴
| an |
| 3n |
| an-1 |
| 3n-1 |
| 2 |
| 3 |
∴数列{
| an |
| 3n |
| 2 |
| 3 |
∴
| an |
| 3n |
| 2 |
| 3 |
∴an=(2n+1)•3n-1.
故答案为:(2n+1)•3n-1.
点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
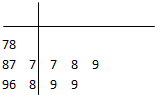 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶): 某正三棱锥的三视图如图所示,则该正三棱锥侧视图的面积为
某正三棱锥的三视图如图所示,则该正三棱锥侧视图的面积为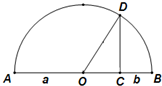 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式