题目内容
下列命题中,真命题的是( )
| A、?x∈R,x2>0 |
| B、?x∈R,-1<sinx<1 |
| C、?x0∈R,2x0<0 |
| D、?x0∈R,tanx0=2 |
考点:特称命题,全称命题
专题:简易逻辑
分析:根据含有量词的命题的判断方法即可得到结论.
解答:
解:A.当x=0时,x2>0不成立,即A错误.
B.当x=
时,-1<sinx<1不成立,即B错误.
C.?x∈R,2X>0,即C错误.
D.∵tanx的值域为R,∴?x0∈R,tanx0=2成立.
故选:D.
B.当x=
| π |
| 2 |
C.?x∈R,2X>0,即C错误.
D.∵tanx的值域为R,∴?x0∈R,tanx0=2成立.
故选:D.
点评:本题主要考查含有量词的命题的真假判断,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“α=
”是“cos2α=0”的( )
| π |
| 4 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不是充分条件也不是必要条件 |
圆锥的底面半径是r,高是h,在这个圆锥内部有一个正方体.正方体的一个面在圆锥的底面上,与这个面相对的面的四个顶点在圆锥的侧面上,则此正方体的棱长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={x|-1<2x+1<5},集合B={x|y=lg(1-x2)},则( )
| A、A⊆B | B、B⊆A |
| C、A∪B=B | D、A∩B=A |
一个几何体的三视图如图,则该几何体的体积为( )


| A、6π+4 |
| B、12π+4 |
| C、6π+12 |
| D、12π+12 |
已知复数满足i3Z=1+2i,则Z等于( )
| A、-2-i | B、-2+i |
| C、2+i | D、2-i |
已知cosα-sinα=-
,α∈(0,π),则tanα=( )
| 2 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
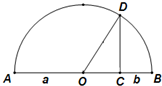 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式