题目内容
己知定义在R上的函数y=f(x)满足f(x)=f(4-x),且当x≠2时,其导函数f′(x)满足f′(x)>
xf′(x),若a∈(2,3),则( )
| 1 |
| 2 |
| A、f(log2a)<f(2a)<f(2) |
| B、f(2a)<f(2)<f(log2a) |
| C、f(2a)<f(log2a)<f(2) |
| D、f(2)<f(log2a)<f(2a) |
考点:函数的单调性与导数的关系
专题:导数的综合应用
分析:根据条件得到函数关于x=2对称,由f′(x)>
xf′(x),得到函数的单调性,利用函数的单调性和对称轴即可得到结论.
| 1 |
| 2 |
解答:
解:∵定义在R上的函数y=f(x)满足f(x)=f(4-x),
∴函数f(x)关于x=2对称,
由f′(x)>
xf′(x),
得(x-2)f′(x)<0,
则x>2时,f′(x)<0,此时函数单调递减,
当x<2时,f′(x)>0,此时函数单调递增.
∴当x=2时,f(x)取得极大值,同时也是最大值.
若a∈(2,3),
则4<2a<8,1<log2a<2,
∴2<4-log2a<3,
∴2<4-log2a<2a,
即f(2)>f(4-log2a)>f(2a),
即f(2a)<f(log2a)<f(2),
故选:C
∴函数f(x)关于x=2对称,
由f′(x)>
| 1 |
| 2 |
得(x-2)f′(x)<0,
则x>2时,f′(x)<0,此时函数单调递减,
当x<2时,f′(x)>0,此时函数单调递增.
∴当x=2时,f(x)取得极大值,同时也是最大值.
若a∈(2,3),
则4<2a<8,1<log2a<2,
∴2<4-log2a<3,
∴2<4-log2a<2a,
即f(2)>f(4-log2a)>f(2a),
即f(2a)<f(log2a)<f(2),
故选:C
点评:本题主要考查函数单调性和对称性的应用,利用导数和函数单调性的关系是解决本题的关键,综合考查函数性质的应用.

练习册系列答案
相关题目
已知集合M={x∈R|-3≤x≤1},N={x∈R|x+1<0},那么M∩N=( )
| A、{-1,0,1} |
| B、{-3,-2,-1} |
| C、{x|-1≤x≤1} |
| D、{x|-3≤x<-1} |
设数列{an}为等差数列,若a1+a3+a13+a15=120,则a8=( )
| A、60 | B、30 | C、20 | D、15 |
已知a,b∈(0,+∞),则“ab>2”是“log2a+log2b>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“α=
”是“cos2α=0”的( )
| π |
| 4 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不是充分条件也不是必要条件 |
圆锥的底面半径是r,高是h,在这个圆锥内部有一个正方体.正方体的一个面在圆锥的底面上,与这个面相对的面的四个顶点在圆锥的侧面上,则此正方体的棱长为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知cosα-sinα=-
,α∈(0,π),则tanα=( )
| 2 |
| A、-1 | ||||
B、-
| ||||
C、
| ||||
| D、1 |
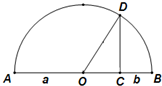 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,请你利用CD≤OD写出一个含有a,b的不等式