题目内容

角α满足条件sinα•cosα＞0，sinα+cosα＜0，则α在（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
考点：三角函数值的符号
专题：三角函数的图像与性质
分析：sinα•cosα＞0得到sinα和cosα同号；再结合sinα+cosα＜0即可得到sinα＜0，cosα＜0；进而得到结论．
解答： 解：因为sinα•cosα＞0
∴sinα和cosα同号．
又∵sinα+cosα＜0
∴sinα＜0，cosα＜0．
即α的正弦和余弦值均为负值．
故α的终边在第三象限．
故选：C．
点评：本题主要考查三角函数值的符号和象限角．是对基础知识的考查，要想做对，需要熟练掌握三角函数值的符号的分布规律．
练习册系列答案
相关题目
如果（y-2）2+|x-4y|=0，则logyx═
 
．
在△ABC中，角A，B，C的对边分别为a，b，c．已知a+b=5，c=
7
，且4sin2
A+B
2
-cos2C=
7
2
．
（1）求角C的大小；
（2）若a＞b，求a，b的值．
已知函数f（x）=|x-1|，x∈R．设a=f[f(
1
2
)]，b=f[f(-
1
2
)]，则（　　）
A、a＞bB、a＜b
C、a=bD、a≠b
已知函数f（x）=a-
1
2x+1
．
（1）求证不论a为何实数，f（x）总是增函数；
（2）若函数f（x）满足f（-x）=-f（x），求f（x）的值域．
若函数f（x）是幂函数，且满足f（4）=3f（2），则f(
1
2
)的值等于
 
．
已知sinα=
3
5
，α∈（
π
2
，π），则cosα=
 
；tan（
π
4
+α）=
 
．
已知α∈(
π
2
，π)，且sinα=
3
5
，则tanα=（　　）
A、
3
4
B、-
3
4
C、
4
3
D、-
4
3
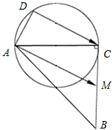如图，已知：|AC|=|BC|=2，∠ACB=90°，M为BC的中点，D为以AC为直径的圆上一动点，则
AM
•
DC
的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网