Question

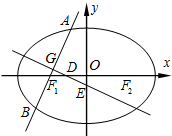如图，已知椭圆C：

x2

a2

+

y2

b2

=1，其左右焦点为F₁（-1，0）及F₂（1，0），过点F₁的直线交椭圆C于A，B两点，线段AB的中点为G，AB的中垂线与x轴和y轴分别交于D，E两点，且|AF₁|、|F₁F₂|、|AF₂|构成等差数列．
（1）求椭圆C的方程；
（2）记△GF₁D的面积为S₁，△OED（O为原点）的面积为S₂．试问：是否存在直线AB，使得S₁=S₂？说明理由．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）依题意，|AF₁|、|F₁F₂|、|AF₂|构成等差数列，求出a，再利用c=1，求出b，即可求椭圆C的方程；
（2）假设存在直线AB，使得 S₁=S₂，确定G，D的坐标，利用△GFD∽△OED，即可得到结论．

解答： 解：（1）因为|AF₁|、|F₁F₂|、|AF₂|构成等差数列，
所以2a=|AF₁|+|AF₂|=2|F₁F₂|=4，所以a=2．…（2分）
又因为c=1，所以b²=3，…（3分）
所以椭圆C的方程为

x2

4

+

y2

3

=1．      …（4分）
（2）假设存在直线AB，使得 S₁=S₂，显然直线AB不能与x，y轴垂直．
设AB方程为y=k（x+1）…（5分）
将其代入

x2

4

+

y2

3

=1，整理得 （4k²+3）x²+8k²x+4k²-12=0…（6分）
设A（x₁，y₁），B（x₂，y₂），所以 x1+x2=

-8k2

4k2+3

．
故点G的横坐标为

x1+x2

2

=

-4k2

4k2+3

．所以G（

-4k2

4k2+3

，

3k

4k2+3

）．…（8分）
因为 DG⊥AB，所以

3k 4k2+3

-4k2 4k2+3 -xD

×k=-1，解得x_D=

-k2

4k2+3

，
即D（

-k2

4k2+3

，0）…（10分）
∵Rt△GDF₁和∵Rt△ODE₁相似，∴若S₁=S₂，则|GD|=|OD|…（11分）
所以 

( -k2 4k2+3 - -4k2 4k2+3 )2+( 3k 4k2+3 )2

=|

-k2

4k2+3

|，…（12分）
整理得 8k²+9=0． …（13分）
因为此方程无解，所以不存在直线AB，使得 S₁=S₂．…（14分）

点评：本题考查直线与椭圆的位置关系，考查韦达定理的运用，考查学生分析解决问题的能力，属于中档题．