题目内容
已知递增等比数列{an}首项a1=2,Sn为其前n项和,且S1,2S2,3S3成等比数列.
(1)求的{an}通项公式;
(2)设bn=
,求数列{bn}的前n项和Tn.
(1)求的{an}通项公式;
(2)设bn=
| 4 |
| anan-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用S1,2S2,3S3成等差数列,确定数列的公比,即可求得数列的通项.
(2)bn=
=
=32n-3,由此利用等比数列求和公式能求出数列{bn}的前n项和Tn.
(2)bn=
| 4 |
| anan-1 |
| 1 | ||||
(
|
解答:
解:(1)设等比数列{an}的公比为q,
∵S1,2S2,3S3成等差数列,
∴4S2=S1+3S3,
∵a1=2,
∴4(2+2q)=2+6(1+q+q2),即3q2-q=0,
解得q=0(舍去)或q=
.
∴an=2•(
)n-1.
(2)∵bn=
=
=32n-3,
∴Tn=3-1+3+33+35+…+32n-3
=
=
(9n-1).
∵S1,2S2,3S3成等差数列,
∴4S2=S1+3S3,
∵a1=2,
∴4(2+2q)=2+6(1+q+q2),即3q2-q=0,
解得q=0(舍去)或q=
| 1 |
| 3 |
∴an=2•(
| 1 |
| 3 |
(2)∵bn=
| 4 |
| anan-1 |
| 1 | ||||
(
|
∴Tn=3-1+3+33+35+…+32n-3
=
| ||
| 1-9 |
=
| 1 |
| 24 |
点评:本题考查等差数列与等比数列的综合,考查数列的通项与求和,属于中档题.

练习册系列答案
相关题目
设等比数列{an}的公比q=2,前n项和为Sn,则
=( )
| S5 |
| a4 |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
已知x,y取值如下表:
从所得散点图中分析可知:y与x线性相关,且
=0.95x+a,则x=13时,y=( )
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
| ∧ |
| y |
| A、1.45 | B、13.8 |
| C、13 | D、12.8 |
设f(x)=x2-4x+3,x∈[1,4],则f(x)的最小值为( )
| A、-1 | B、0 | C、3 | D、-2 |
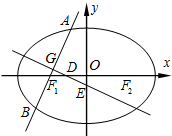 如图,已知椭圆C:
如图,已知椭圆C: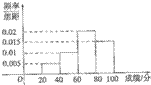 某班的全体学生参加某项技能测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],若不低于80分的人数是8,则该班的学生人数是( )
某班的全体学生参加某项技能测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],若不低于80分的人数是8,则该班的学生人数是( )