题目内容
求下列函数的定义域:f(x)=
+
,定义域为 .
| x+1 |
| 1 |
| 2-x |
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用
分析:由题意可得
,解出可得函数定义域.
|
解答:
解:要使函数f(x)有意义,
须有
,解得x≥-1且x≠2,
∴函数的定义域是[-1,2)∪(2,+∞).
故答案为[-1,2)∪(2,+∞)
须有
|
∴函数的定义域是[-1,2)∪(2,+∞).
故答案为[-1,2)∪(2,+∞)
点评:本题考查函数定义域的求解,属基础题,要求:开偶次方根被开方数要大于等于零;分母不为零.注意定义域的表示形式.

练习册系列答案
相关题目
函数y=ax2+bx与y=ax+b,(ab≠0)的图象只能是( )
A、 |
B、 |
C、 |
D、 |
复数
(i为虚数单位)的实部是( )
| 3+i |
| i2 |
| A、3 | B、-1 | C、-3 | D、-i |
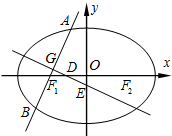 如图,已知椭圆C:
如图,已知椭圆C: