题目内容
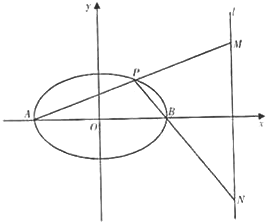 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)求k1•k2的值;
(3)求证:以MN为直线的圆过x轴上的定点,并求出定点的坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由
=
,
=4,能求出椭圆C的方程.
(2)设P(x0,y0),则k1=
,k2=
,由此能求出k1k2=
=-
.
(3)设M(4,y1),N(4,y2),则k1=kAM=
,k2=kAN=
,从而y1y2=-9,由此能证明以MN为直线的圆过x轴上的定点(7,0),(1,0).
| c |
| a |
| 1 |
| 2 |
| a2 |
| c |
(2)设P(x0,y0),则k1=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
| ||
| x02-4 |
| 3 |
| 4 |
(3)设M(4,y1),N(4,y2),则k1=kAM=
| y1 |
| 6 |
| y2 |
| 2 |
解答:
(1)解:∵
=
,
=4,解得a=2,c=1,
∴b=
,
∴椭圆C的方程为
+
=1.
(2)解:设P(x0,y0),∵A(-2,0),B(2,0),
∴k1=
,k2=
,
∴k1k2=
,
∵P(x0,y0)在椭圆上,∴
+
=1,
∴y02=
(4-x02),
∴k1k2=
=-
.
(3)证明:设M(4,y1),N(4,y2),
则k1=kAM=
,k2=kAN=
,
∴k1k2=
,
又k1k2=-
,∴
=-
,∴y1y2=-9,
∵MN的中点为Q(4,
),NM=|y1-y2|,
∴以MN为直径的圆方程为(x-4)2+(y-
)2=
,
令y=0,得(x-4)2=-y1y2=9,
解得x=1或x=7,
∴以MN为直线的圆过x轴上的定点(7,0),(1,0).
| c |
| a |
| 1 |
| 2 |
| a2 |
| c |
∴b=
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)解:设P(x0,y0),∵A(-2,0),B(2,0),
∴k1=
| y0 |
| x0+2 |
| y0 |
| x0-2 |
∴k1k2=
| y02 |
| x02-4 |
∵P(x0,y0)在椭圆上,∴
| x02 |
| 4 |
| y02 |
| 3 |
∴y02=
| 3 |
| 4 |
∴k1k2=
| ||
| x02-4 |
| 3 |
| 4 |
(3)证明:设M(4,y1),N(4,y2),
则k1=kAM=
| y1 |
| 6 |
| y2 |
| 2 |
∴k1k2=
| y1y2 |
| 12 |
又k1k2=-
| 3 |
| 4 |
| y1y2 |
| 12 |
| 3 |
| 4 |
∵MN的中点为Q(4,
| y1+y2 |
| 2 |
∴以MN为直径的圆方程为(x-4)2+(y-
| y1+y2 |
| 2 |
| (y1-y2)2 |
| 4 |
令y=0,得(x-4)2=-y1y2=9,
解得x=1或x=7,
∴以MN为直线的圆过x轴上的定点(7,0),(1,0).
点评:本题考查椭圆方程的求法,考查两直线的斜率乘积为定值的求法,考查以MN为直线的圆过x轴上的定点的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
命题p:2+2=5; 命题q:3>2,则下列各项中,正确的是( )
| A、p或q为真命题,q为假命题 |
| B、p且q为假命题,¬q为真命题 |
| C、p且q为假命题,¬q为假命题 |
| D、p且q为假命题,p或q为假命题 |
设等比数列{an}的公比q=2,前n项和为Sn,则
=( )
| S5 |
| a4 |
| A、2 | ||
| B、4 | ||
C、
| ||
D、
|
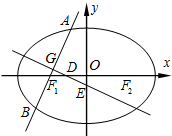 如图,已知椭圆C:
如图,已知椭圆C: