题目内容
有以下命题:
①一个简谐运动的函数表达式为f(x)=sin(
x+
),则这个简谐运动的函数的最小正周期为4π;
②已知函数f(x)=loga(x-
)+89,(a>0且a≠1)恒过定点(m,n),则m,n使等式m=sin21°+sin22°+sin23°+…+sin2n°成立;
③对于函数f(x)=x2+ax+b和g(x)=logax(0<a<1),有f(
)≤f(x1)+f(x2)和g(
)≥g(x1)+g(x2)成立;
④定义:若任意x∈A,总有a-x∈A,(A≠∅),就称集合A为a的闭集.已知集合A⊆{1,2,3,4,5,6},且A为6的闭集,则这样的集合A共有7个;
其中所有正确叙述的命题序号是 .
①一个简谐运动的函数表达式为f(x)=sin(
| 1 |
| 2 |
| 3π |
| 4 |
②已知函数f(x)=loga(x-
| 87 |
| 2 |
③对于函数f(x)=x2+ax+b和g(x)=logax(0<a<1),有f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
④定义:若任意x∈A,总有a-x∈A,(A≠∅),就称集合A为a的闭集.已知集合A⊆{1,2,3,4,5,6},且A为6的闭集,则这样的集合A共有7个;
其中所有正确叙述的命题序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:利用函数的周期判断①的正误;求出函数经过的定点然后判断等式是否成立判断②的正误;利用函数的凹凸性判断③的正误;根据已知中“闭集”的定义,求出集合A⊆{1,2,3,4,5,6}且A为6的“闭集”,可判断④的正误;
解答:
解:对于①,一个简谐运动的函数表达式为f(x)=sin(
x+
),则这个简谐运动的函数的最小正周期为4π;∴①正确;
对于②,已知函数f(x)=loga(x-
)+89,(a>0且a≠1)恒过定点(m,n),则m=
,n=89,
使等式m=sin21°+sin22°+sin23°+…+sin289°成立;
(∵sin21°+sin22°+sin23°+…+sin289+cos21°+cos22°+cos23°+…+cos289°=89,∴m=
)∴②正确;
对于③,对于函数f(x)=x2+ax+b是凹函数和g(x)=logax(0<a<1),是凸函数,有f(
)≤f(x1)+f(x2)和g(
)≥g(x1)+g(x2)成立,∴③正确;
对于④,集合A⊆{1,2,3,4,5,6}且A为6的“闭集”,则这样的集合A共有
{3},{1,5},{2,4},{1,3,5},{2,3,4},{1,2,4,5},{1,2,3,4,5}共7个,故④正确.
故答案为:①②③④.
| 1 |
| 2 |
| 3π |
| 4 |
对于②,已知函数f(x)=loga(x-
| 87 |
| 2 |
| 89 |
| 2 |
使等式m=sin21°+sin22°+sin23°+…+sin289°成立;
(∵sin21°+sin22°+sin23°+…+sin289+cos21°+cos22°+cos23°+…+cos289°=89,∴m=
| 89 |
| 2 |
对于③,对于函数f(x)=x2+ax+b是凹函数和g(x)=logax(0<a<1),是凸函数,有f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
对于④,集合A⊆{1,2,3,4,5,6}且A为6的“闭集”,则这样的集合A共有
{3},{1,5},{2,4},{1,3,5},{2,3,4},{1,2,4,5},{1,2,3,4,5}共7个,故④正确.
故答案为:①②③④.
点评:本题考查的知识点是三周函数的周期性,三角函数值的求法,函数凹凸性,是逻辑与其它章节的综合应用,难度中档.

练习册系列答案
相关题目
在区间[-2,2]上随机取一个数m,则直线y=x+m与圆x2+y2=2x相交的概率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
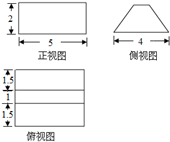

A、
| ||
| B、50cm3 | ||
C、
| ||
| D、25cm3 |
设a=log210,b=log315,c=log735,则( )
| A、c>a>b |
| B、b>c>a |
| C、b>a>c |
| D、a>b>c |
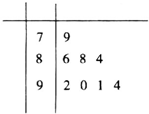 某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是
某校对高一年级8个班参加合唱比赛的得分进行了统计,得到样本的茎叶图(如图所示),则该样本的中位数和平均数分别是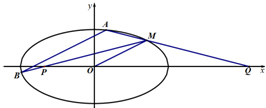 如图,已知离心率为
如图,已知离心率为