题目内容
已知椭圆方程为
+
=1,则以点P(2,-1)为中点的弦所在直线方程 .
| x2 |
| 16 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设以P(2,-1)为中点的弦与椭圆交于A(x1,y1),B(x2,y2),利用点差法能求出结果.
解答:
解:设以点P(2,-1)为中点的弦与椭圆交于A(x1,y1),B(x2,y2),
则x1+x2=4,y1+y2=-2,
分别把A(x1,y1),B(x2,y2)代入椭圆方程为
+
=1,
得
,∴(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0,
∴4(x1-x2)-8(y1-y2)=0,
∴k=
=
,
∴点P(2,-1)为中点的弦所在直线方程为y+1=
(x-2),
整理,得:x-2y-4=0.
故答案为:x-2y-4=0.
则x1+x2=4,y1+y2=-2,
分别把A(x1,y1),B(x2,y2)代入椭圆方程为
| x2 |
| 16 |
| y2 |
| 4 |
得
|
∴4(x1-x2)-8(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
∴点P(2,-1)为中点的弦所在直线方程为y+1=
| 1 |
| 2 |
整理,得:x-2y-4=0.
故答案为:x-2y-4=0.
点评:本题考查直线方程的求法,是中档题,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
在△ABC中,A=
,BC=
,则“AC=
”是“B=
”的( )
| π |
| 4 |
| 2 |
| 3 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
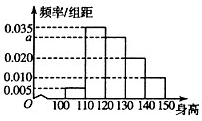 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[l40,150]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[120,130)的学生中选取的人数应为
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[l40,150]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[120,130)的学生中选取的人数应为