题目内容

设a=log210，b=log315，c=log735，则（　　）
A、c＞a＞b
B、b＞c＞a
C、b＞a＞c
D、a＞b＞c
考点：对数的运算性质
专题：函数的性质及应用
分析：由对数的运算性质可得a=log210＞3，2＜b＜3，c=log735＜2，从而得到a、b、c的大小关系．
解答： 解：由对数的性质可得a=log210＞log28=3，log39=2＜b=log315＜log327，
c=log735＜log749=2，
∴a＞b＞c，
故选：D．
点评：本题主要考查对数的运算性质、对数函数的单调性，属于基础题．
练习册系列答案
相关题目
设函数f（x）=
1
1-x
的定义域为M，则∁RM=（　　）
A、（-∞，1）
B、（1，+∞）
C、（-∞，1]
D、[1，+∞）
有以下命题：
①一个简谐运动的函数表达式为f(x)=sin(
1
2
x+
3π
4
)，则这个简谐运动的函数的最小正周期为4π；
②已知函数f（x）=loga(x-
87
2
)+89，(a＞0且a≠1)恒过定点（m，n），则m，n使等式m=sin21°+sin22°+sin23°+…+sin2n°成立；
③对于函数f（x）=x2+ax+b和g(x)=logax(0＜a＜1)，有f(
x1+x2
2
)≤f(x1)+f(x2)和g(
x1+x2
2
)≥g(x1)+g(x2)成立；
④定义：若任意x∈A，总有a-x∈A，（A≠∅），就称集合A为a的闭集．已知集合A⊆{1，2，3，4，5，6}，且A为6的闭集，则这样的集合A共有7个；
其中所有正确叙述的命题序号是
 
．
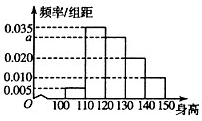从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[120，130），[130，140），[l40，150]三组内的学生中，用分层抽样的方法选取30人参加一项活动，则从身高在[120，130）的学生中选取的人数应为
 
．
若F1、F2是双曲线
x2
4
-
y2
5
=1的两个焦点，点P是该双曲线上一点，满足|PF1|+|PF2|=9，则|PF1|•|PF2|=（　　）
A、4
B、5
C、
65
4
D、2
已知F1，F2分别是椭圆的左，右焦点，现以F2为圆心作一个圆恰好经过椭圆中心并且交椭圆于点M，N，若过F1的直线MF1是圆F2的切线，则椭圆的离心率为（　　）
A、
3
-1
B、2-
3
C、
2
2
D、
3
2
cos
π
9
•cos
2π
9
•cos（-
23π
9
）=（　　）
A、-
1
8
B、-
1
16
C、
1
16
D、
1
8
在对某渔业产品的质量调研中，从甲、乙两地出产的该产品中各随机抽取10件，测量该产品中某种元素的含量（单位：毫克）．如图是测量数据的茎叶图：

规定：当产品中的此种元素含量≥15毫克时为优质品．
（Ⅰ）试用上述样本数据估计甲、乙两地该产品的优质品率（优质品件数/总件数）；
（Ⅱ）从乙地抽出的上述10件产品中，随机抽取3件，求抽到的3件产品中优质品数ξ的分布列及数学期望E（ξ）．
如图所示，F1、F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，
3
2
）到F1、F2两点的距离之和为4．
（1）求椭圆C的方程和焦点坐标；
（2）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求弦长|PQ|．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网