题目内容
已知函数f(x)=
x3-
(a+1)x2+ax.
(1)求f(x)的单调区间.
(2)方程f(x)=0仅有一个零点,求实数a的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(1)求f(x)的单调区间.
(2)方程f(x)=0仅有一个零点,求实数a的取值范围.
考点:利用导数研究函数的单调性,函数的零点
专题:导数的综合应用
分析:(1)通过讨论a的范围,从而得到函数的单调区间;(2)通过讨论a>1,a<1,根据极小值大于0,从而得到a的范围.
解答:
解:(1)f′(x)=x2-(a+1)x+a=(x-1)(x-a),
当a>1时,由f′(x)>0得x<1或x>a,
∴x∈(-∞,1)和(a,+∞)时,f(x)单调递增,x∈(1,a)时,f(x)单调递减;
当a<1时,由f′(x)>0,得x<a或x>1,
∴x∈(-∞,a)和(1,+∞)时,f(x)单调递增,x∈(a,1)时,f(x)单调递减;
(2)由(1)知x=1和x=a是f(x)得极值点,
a>1时,f(1)是极大值,f(a)是极小值;
只需f(a)>0,解得:a<1,不合题意,
a<1时,f(a)是极大值,f(1)是极小值,
只需f(1)>0,解得:
<a<1,
故a的范围是:(
,1).
当a>1时,由f′(x)>0得x<1或x>a,
∴x∈(-∞,1)和(a,+∞)时,f(x)单调递增,x∈(1,a)时,f(x)单调递减;
当a<1时,由f′(x)>0,得x<a或x>1,
∴x∈(-∞,a)和(1,+∞)时,f(x)单调递增,x∈(a,1)时,f(x)单调递减;
(2)由(1)知x=1和x=a是f(x)得极值点,
a>1时,f(1)是极大值,f(a)是极小值;
只需f(a)>0,解得:a<1,不合题意,
a<1时,f(a)是极大值,f(1)是极小值,
只需f(1)>0,解得:
| 1 |
| 6 |
故a的范围是:(
| 1 |
| 6 |
点评:本题考查了函数的单调性,考查了导数的应用,考查了分类讨论思想,是一道中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
tan(-
)=( )
| 17π |
| 6 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知a,b表示直线,α,β表示平面,下列推理正确的是( )
| A、α∩β=a,b?α⇒a∥b |
| B、α∩β=a,a∥b⇒b∥α且b∥β |
| C、a∥β,b∥β,a?α,b?α⇒α∥β |
| D、α∥β,α∩γ=a,β∩γ=b⇒a∥b |
椭圆
+
=1的两个焦点为F1、F2,点P是椭圆上任意一点(非左右顶点),在△PF1F2的周长为( )
| x2 |
| 9 |
| y2 |
| 5 |
| A、6 | B、8 | C、10 | D、12 |

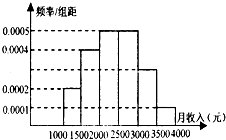 为征求个人所得税法修改建议,某机构对当地居民的月收入调查10000人,根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),因操作人员不慎,未标出第五组顶部对应的纵轴数据.
为征求个人所得税法修改建议,某机构对当地居民的月收入调查10000人,根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)),因操作人员不慎,未标出第五组顶部对应的纵轴数据.