题目内容
已知a,b表示直线,α,β表示平面,下列推理正确的是( )
| A、α∩β=a,b?α⇒a∥b |
| B、α∩β=a,a∥b⇒b∥α且b∥β |
| C、a∥β,b∥β,a?α,b?α⇒α∥β |
| D、α∥β,α∩γ=a,β∩γ=b⇒a∥b |
考点:空间中直线与平面之间的位置关系,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间线面关系及面面关系定理,对选项分别分析解答.
解答:
解:对于选项A,α∩β=a,b?α,直线a,b可能相交;故A错误;
对于选项B,α∩β=a,a∥b,直线b可能在两个平面内,故B错误;
对于选项C,a∥β,b∥β,a?α,b?α,直线a,b如果不相交,α,β可能相交,故C错误;
对于选项D,根据面面平行的性质以及α∥β,α∩γ=a得到a∥β,β∩γ=b进一步得到a∥b;故D正确;
故选D.
对于选项B,α∩β=a,a∥b,直线b可能在两个平面内,故B错误;
对于选项C,a∥β,b∥β,a?α,b?α,直线a,b如果不相交,α,β可能相交,故C错误;
对于选项D,根据面面平行的性质以及α∥β,α∩γ=a得到a∥β,β∩γ=b进一步得到a∥b;故D正确;
故选D.
点评:本题考查了空间线面平行的性质和判定定理的运用,熟练相关的性质定理和判定定理是关键,属于中档题.

练习册系列答案
相关题目
已知 f(x)=|lgx|,若0<a<1<b且f(a)=f(b),则log2(1+ab)的值为( )
| A、0 | B、1 | C、-1 | D、不确定 |
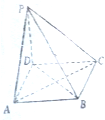 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=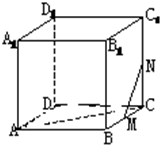 在正方体ABCD-A1B1C1D1中,求证:
在正方体ABCD-A1B1C1D1中,求证: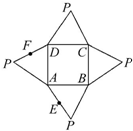 如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论: 已知正三棱锥S-ABC内接于半径为4的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如下,则此三棱锥的体积为
已知正三棱锥S-ABC内接于半径为4的球,过侧棱SA及球心O的平面截三棱锥及球面所得截面如下,则此三棱锥的体积为