Question

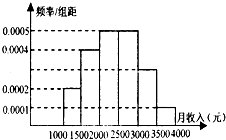为征求个人所得税法修改建议，某机构对当地居民的月收入调查10000人，根据所得数据画了样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示收入在[1000，1500）），因操作人员不慎，未标出第五组顶部对应的纵轴数据．
（Ⅰ）请你补上第五组顶部对应的纵轴数据，并求居民月收入在[3000，4000）的频率；
（Ⅱ）根据频率分布直方图估算样本数据的中位数；
（Ⅲ）为了分析居民收入与年龄、职业等方面的关系，必须按月收入再从这10000人中用分层抽样方法抽出100人进行分析，则月收入在[2500，3000）的这段应抽多少人？

Answer 1

考点：频率分布表,频率分布直方图

专题：概率与统计

分析：（1）求出第五组顶部对应的纵轴数据，计算出居民收入在[3000，4000）的频率；
（2）判断样本数据的中位数在第三组中，求出中位数；
（3）求出第四组的人数，计算出月收入在[2500，3000）的这段应抽的人数．

解答： 解：（1）第五组顶部对应的纵轴数据为：
1÷500-0.0002-0.0004-0.0005×2-0.0001=0.0003，
居民收入在[3000，4000）的频率为
1-（0.10+0.20+0.25+0.25）=0.2；
（2）第一组和第二组的频率之和为
（0.0002+0.0004）×500=0.3，
第三组的频率为0.0005×500=0.25，
因此，可以估算样本数据的中位数在第三组中，设为x，
则（x-2000）×0.0005+0.3=0.5，
解得中位数为x=2400；
（3）第四组的人数为0.0005×500×10000=2500，
因此月收入在[2500，3000）的这段应抽
2500×

100

10000

=25（人）

点评：本题考查了频率分布直方图的应用问题，解题时应根据直方图进行有关的计算，是基础题．