题目内容
用min{a,b,c}表示a,b,c三个数中的最小值,设f(x)=min{2x,x+1,10-x}(x≥0),则f(x)的最大值为 .
考点:分段函数的应用
专题:函数的性质及应用
分析:在同一坐标系内画出三个函数y=10-x,y=x+1,y=2x的图象,以此确定出函数f(x)图象,观察最大值的位置,通过求函数值,解出最大值.
解答:
解:f(x)=min{2x,x+1,10-x}(x≥0)如图所示,

则f(x)的最大值为y=x+1与y=10-x交点的纵坐标,
由
得A(
,
)
即当x=
时,y=
.
故答案为:
.

则f(x)的最大值为y=x+1与y=10-x交点的纵坐标,
由
|
| 9 |
| 2 |
| 11 |
| 2 |
即当x=
| 9 |
| 2 |
| 11 |
| 2 |
故答案为:
| 11 |
| 2 |
点评:本题考查了函数的概念、图象、最值问题.利用了数形结合的方法.关键是通过题意得出f(x)的简图.

练习册系列答案
相关题目
已知二次函数y=x2+mx+4,当x∈R时,恒有y>0,则m的取值范围是( )
| A、(0,2) |
| B、(-2,2) |
| C、(-4.4) |
| D、(-2,0) |
已知 f(x)=|lgx|,若0<a<1<b且f(a)=f(b),则log2(1+ab)的值为( )
| A、0 | B、1 | C、-1 | D、不确定 |
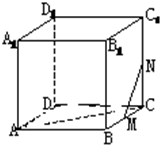 在正方体ABCD-A1B1C1D1中,求证:
在正方体ABCD-A1B1C1D1中,求证: