题目内容
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;
③在△ABC中,“A>45°”是“sinA>
”的充要条件.
④命题“?x0∈R,ex0≤0”是真命题.其中正确的命题的个数是 .
①若“p且q”为假命题,则p、q均为假命题;
②命题“若x≥2且y≥3,则x+y≥5”的否命题为“若x<2且y<3,则x+y<5”;
③在△ABC中,“A>45°”是“sinA>
| ||
| 2 |
④命题“?x0∈R,ex0≤0”是真命题.其中正确的命题的个数是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①若“p且q”为假命题,则p、q中至少有一个为假命题,即可判断出;
②命题“若x≥2且y≥3,则x+y≥5”的否命题应为“若x<2或y<3,则x+y<5”;
③在△ABC中,“sinA>
”⇒“A>45°”,反之不成立,即可判断出;
④由于?x∈R,都有ex>0.可得命题“?x0∈R,ex0≤0”的真假.
②命题“若x≥2且y≥3,则x+y≥5”的否命题应为“若x<2或y<3,则x+y<5”;
③在△ABC中,“sinA>
| ||
| 2 |
④由于?x∈R,都有ex>0.可得命题“?x0∈R,ex0≤0”的真假.
解答:
解:①若“p且q”为假命题,则p、q中至少有一个为假命题,因此①不正确;
②命题“若x≥2且y≥3,则x+y≥5”的否命题应为“若x<2或y<3,则x+y<5”,因此不正确;
③在△ABC中,“sinA>
”⇒“A>45°”,反之不成立,因此“A>45°”是“sinA>
”的必要不充分条件,不正确.
④∵?x∈R,都有ex>0.∴命题“?x0∈R,ex0≤0”是假命题.
综上可知:没有正确的命题.
故答案为:0.
②命题“若x≥2且y≥3,则x+y≥5”的否命题应为“若x<2或y<3,则x+y<5”,因此不正确;
③在△ABC中,“sinA>
| ||
| 2 |
| ||
| 2 |
④∵?x∈R,都有ex>0.∴命题“?x0∈R,ex0≤0”是假命题.
综上可知:没有正确的命题.
故答案为:0.
点评:本题考查了简易逻辑的有关知识,属于基础题.

练习册系列答案
相关题目
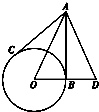 如图,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于
如图,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,那么∠ADO等于