题目内容

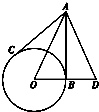如图，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD=OB，连接AD．如果∠DAC=78°，那么∠ADO等于
 
．
考点：与圆有关的比例线段
专题：直线与圆
分析：由已知条件推导出∠CAO=∠OAB=∠BAD，∠ABD=90°，由此根据∠DAC=78°，能求出∠ADO的大小．
解答： 解：∵AB、AC为⊙O的切线，B和C是切点，
延长OB到D，使BD=OB，连接AD，
∴∠CAO=∠OAB=∠BAD，∠ABD=90°，
∵∠DAC=78°，
∴∠BAD=
1
3
∠DAC=26°，
∴∠ADO=90°-26°=64°．
故答案为：64°．
点评：本题考查角的大小的求法，是中档题，解题时要认真审题，注意切线性质的灵活运用．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），左、右两个焦点分别为F1、F2，上顶点M（0，b），△MF1F2为正三角形且周长为6，直线l：x=my+4与椭圆C相交于A、B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求
OA
•
OB
的取值范围．
已知正三棱锥S-ABC的外接球的表面积为36π，M、N分别是SC、BC的中点，且MN⊥AM，则此三棱锥的侧棱SA=
 
．
下列命题中，正确命题的序号是
 
．
①函数y=sin4x-cos4x的最小正周期是π；
②终边在y轴上的角的集合是{α|α=
kπ
2
，k∈Z}；
③在同一坐标系中，函数y=sinx的图象与函数y=x的图象有3个公共点；
④把函数y=3sin（2x+
π
3
）的图象向右平移
π
6
得到y=3sin2x的图象．
设实数x，y满足约束条件：
x≥2
y≥x
2x+y≤12
，则z=x2+y2的最大值为
 
．
已知抛物线C1：y=-
1
2p
x2（p＞0）的焦点与双曲线C2：
x2
3
-y2=1的左焦点的连线交C1于第三象限的点M．若C1在点M处的切线平行于C2的一条渐近线，则P=
 
．
给出如下四个命题：
①若“p且q”为假命题，则p、q均为假命题；
②命题“若x≥2且y≥3，则x+y≥5”的否命题为“若x＜2且y＜3，则x+y＜5”；
③在△ABC中，“A＞45°”是“sinA＞
2
2
”的充要条件．
④命题“?x0∈R，ex0≤0”是真命题．其中正确的命题的个数是
 
．
有下列命题：
①已知函数f（x）为连续可导函数，若f（x）为奇函数，则f（x）的导函数f′（x）为偶函数；
②若函数f（x）=x2，则f′（2x）=[f（2x）]′；
③若函数g（x）=（x-1）（x-2）…（x-5）（x-6），则g′（6）=120；
④若三次函数f（x）=ax3+bx2+cx+d，则“a+b+c=0”是“f（x）有极值”的充要条件．
其中真命题的序号是
 
．
若x、y满足条件
3x-5y+6≥0
2x+3y-15≤0
y≥0
，当且仅当x=y=3时，z=ax-y取最小值，则实数a的取值范围是（　　）
A、(-
2
3
，
3
5
)
B、(-
2
3
，
3
4
)
C、(-
3
4
，
2
3
)
D、(
3
4
，
3
5
)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网