题目内容
设F为抛物线y2=2x的焦点,A、B、C为抛物线上三点,若F为△ABC的重心,则|
|+|
|+|
|的值为( )
| FA |
| FB |
| FC |
| A、1 | B、2 | C、3 | D、4 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),C(x3,y3),由已知条件推导出x1+x2+x3=
,|
|=x1+
,|
|=x2+
,|
|=x3+
,由此能求出|
|+|
|+|
|的值.
| 3 |
| 2 |
| FA |
| 1 |
| 2 |
| FB |
| 1 |
| 2 |
| FC |
| 1 |
| 2 |
| FA |
| FB |
| FC |
解答:
解:设A(x1,y1),B(x2,y2),C(x3,y3)
抛物线y2=2x焦点坐标F(
,0),准线方程:x=-
,
∵点F(
,0)是△ABC重心,
∴x1+x2+x3=
,y1+y2+y3=0,
而|
|=x1-(-
)=x1+
,
|
|=x2-(-
)=x2+
,
|
|=x3-(-
)=x3+
,
∴|
|+|
|+|
|=x1+
+x2+
+x3+
=(x1+x2+x3)+
=
+
=3.
故选:C.
抛物线y2=2x焦点坐标F(
| 1 |
| 2 |
| 1 |
| 2 |
∵点F(
| 1 |
| 2 |
∴x1+x2+x3=
| 3 |
| 2 |
而|
| FA |
| 1 |
| 2 |
| 1 |
| 2 |
|
| FB |
| 1 |
| 2 |
| 1 |
| 2 |
|
| FC |
| 1 |
| 2 |
| 1 |
| 2 |
∴|
| FA |
| FB |
| FC |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=(x1+x2+x3)+
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
故选:C.
点评:本题考查抛物线的简单性质的应用,是中档题,解题时要认真审题,注意三角形重心性质的灵活运用.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
设x,y满足约束条件
,则z=3x+y的最大值是( )
|
| A、0 | B、4 | C、5 | D、6 |
若x、y满足条件
,当且仅当x=y=3时,z=ax-y取最小值,则实数a的取值范围是( )
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|
已知实数a,b满足:-1<a-b<3且2<a+b<4,则2a-3b的取值范围是( )
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
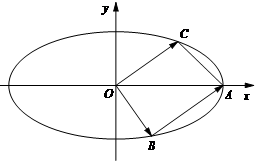 如图,已知椭圆
如图,已知椭圆