题目内容
下列命题:
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.
②若p为:?x∈R,x2+2x≤0,则¬p为:?x∈R,x2+2x>0.
③命题“?x,x2-2x+3>0”的否命题是“?x,x2-2x+3<0”.
④命题“若¬p则q”的逆否命题是“若p,则¬q”.
其中正确结论的序号是 .
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.
②若p为:?x∈R,x2+2x≤0,则¬p为:?x∈R,x2+2x>0.
③命题“?x,x2-2x+3>0”的否命题是“?x,x2-2x+3<0”.
④命题“若¬p则q”的逆否命题是“若p,则¬q”.
其中正确结论的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①由“或命题”“且命题”的意义及其关系、充分必要条件即可判断出;
②由非命题的定义即可判断出;
③由非命题的意义即可得出;
④由逆否命题的意义即可得出.
②由非命题的定义即可判断出;
③由非命题的意义即可得出;
④由逆否命题的意义即可得出.
解答:
解:①p,q为两个命题,由“p且q为真”⇒“p或q为真”,反之不成立,因此“p且q为真”是“p或q为真”的充分不必要条件. 因此不正确.
②若p为:?x∈R,x2+2x≤0,由非命题的定义可得:¬p为:?x∈R,x2+2x>0,可知正确.
③命题“?x,x2-2x+3>0”的非命题是“?x,x2-2x+3≤0”,可知③不正确.
④命题“若¬p则q”的逆否命题是“若¬q,则p”,因此不正确.
综上可知:只有①②正确.
故答案是:②.
②若p为:?x∈R,x2+2x≤0,由非命题的定义可得:¬p为:?x∈R,x2+2x>0,可知正确.
③命题“?x,x2-2x+3>0”的非命题是“?x,x2-2x+3≤0”,可知③不正确.
④命题“若¬p则q”的逆否命题是“若¬q,则p”,因此不正确.
综上可知:只有①②正确.
故答案是:②.
点评:本题考查了简易逻辑的有关知识,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=x2+bx+c且f(1+x)=f(-x),则下列不等式中成立的是( )
| A、f(-2)<f(0)<f(2) |
| B、f(0)<f(-2)<f(2) |
| C、f(2)<f(0)<f(-2) |
| D、f(0)<f(2)<f(-2) |
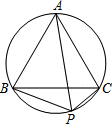 如图,P是等边△ABC外接圆
如图,P是等边△ABC外接圆