题目内容
[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x],(x∈R),g(x)=log4(x-1),则函数h(x)=f(x)-g(x)的零点个数为( )
| A、4 | B、3 | C、2 | D、1 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由f(x+2)=f(x),得到函数的周期是2,作出函数f(x)和g(x)的图象,利用数形结合即可得到结论.
解答:
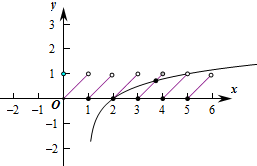 解:当0<x<1时,[x]=0,则f(x)=x-[x]=x,
解:当0<x<1时,[x]=0,则f(x)=x-[x]=x,
当1≤x<2时,[x]=1,则f(x)=x-[x]=x-1,
当2≤x<3时,[x]=2,则f(x)=x-[x]=x-2,
当3≤x<4时,[x]=3,则f(x)=x-[x]=x-3,
当4≤x<5时,[x]=4,则f(x)=x-[x]=x-4,
当5≤x<6时,[x]=5,则f(x)=x-[x]=x-5,此时f(x)∈[0,1),而g(x)log4(x-1)≥1,
即当n≤x<n+1,n≥6时,[x]=n,则f(x)=x-[x]=x-n∈[0,1),而g(x)log4(x-1)≥1,
由h(x)=f(x)-g(x)=0得f(x)=g(x),
分别作出函数f(x)和g(x)的图象如图:
则两个函数图象有2个交点,
故函数零点的个数为2个,
故选:C
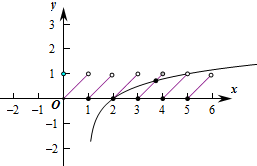 解:当0<x<1时,[x]=0,则f(x)=x-[x]=x,
解:当0<x<1时,[x]=0,则f(x)=x-[x]=x,当1≤x<2时,[x]=1,则f(x)=x-[x]=x-1,
当2≤x<3时,[x]=2,则f(x)=x-[x]=x-2,
当3≤x<4时,[x]=3,则f(x)=x-[x]=x-3,
当4≤x<5时,[x]=4,则f(x)=x-[x]=x-4,
当5≤x<6时,[x]=5,则f(x)=x-[x]=x-5,此时f(x)∈[0,1),而g(x)log4(x-1)≥1,
即当n≤x<n+1,n≥6时,[x]=n,则f(x)=x-[x]=x-n∈[0,1),而g(x)log4(x-1)≥1,
由h(x)=f(x)-g(x)=0得f(x)=g(x),
分别作出函数f(x)和g(x)的图象如图:
则两个函数图象有2个交点,
故函数零点的个数为2个,
故选:C
点评:本题主要考查函数零点个数的判断,根据[x]的定义,求出函数f(x)的表达式,利用数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有两排座位,前排11个座位,后排10个座位.现安排2人就坐,规定前排中间的3个座位不能坐,那么不同排法的种数是( )
| A、234 | B、276 |
| C、306 | D、363 |
已知|
|=1,|
|=
,(
-
)•
=0,则
与
的夹角是( )
| a |
| b |
| 2 |
| a |
| b |
| a |
| a |
| b |
| A、60° | B、90° |
| C、45° | D、30° |
已知x>0,y>0,2x+3y=1,则4x+8y的最小值为( )
| A、8 | ||
| B、6 | ||
C、2
| ||
D、3
|
Z=x+yi(x,y∈R),当|Z|=1时,x,y满足y-kx+2k=0,则k的取值范围( )
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
一物体的运动方程为s=sin2t+3t+1,则它的速度方程为( )
| A、v=2cos2t+3 |
| B、v=2sin2t+3 |
| C、v=-2cos2t+3 |
| D、v=2cos2t+3t+1 |
对于两条不同的直线a,b和平面β,若a⊥β,则“a∥b“是“b⊥β”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分又不必要条件 |
用总长为120cm的钢条围成一个长方体的框架,要求长方体底面边长比是2:3,当长方体的体积最大时,长方体的高为( )
| A、4cm | B、6cm |
| C、8cm | D、10cm |
