题目内容
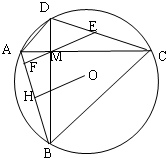 如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证:
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M,AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,求证:(1)EF⊥AB
(2)OH=ME.
考点:与圆有关的比例线段
专题:直线与圆
分析:(1)由已知条件推导出ME=CE,∠CME=∠MCB,从而得到∠AMF=∠ABM,由此能够证明EF⊥AB.
(2)由已知条件推导出EF∥OH,HM∥OE,从而得到四边形HMEO是平行四边形,由此能够证明OH=ME.
(2)由已知条件推导出EF∥OH,HM∥OE,从而得到四边形HMEO是平行四边形,由此能够证明OH=ME.
解答:
证明:(1)∵AC⊥BD,CE=DE,
∴ME=CE,∠CME=∠MCB,
∵∠ABM=∠MCB,∠AMF=∠EMC,
∴∠AMF=∠ABM,
∴∠FAM+∠AMF=∠ABM+MAB=90°,
∴EF⊥AB.
(2)∵E是CD的中点,∴OE⊥CD,OH⊥AB,
由(1)EF⊥AB,又OH⊥AB,
EF∥OH,同理,HM∥OE,
∴四边形HMEO是平行四边形,
∴OH=ME.

∴ME=CE,∠CME=∠MCB,
∵∠ABM=∠MCB,∠AMF=∠EMC,
∴∠AMF=∠ABM,
∴∠FAM+∠AMF=∠ABM+MAB=90°,
∴EF⊥AB.
(2)∵E是CD的中点,∴OE⊥CD,OH⊥AB,
由(1)EF⊥AB,又OH⊥AB,
EF∥OH,同理,HM∥OE,
∴四边形HMEO是平行四边形,
∴OH=ME.
点评:本题考查直线垂直的证明,考查线段相等的证明,解题时要认真审题,注意圆的性质的灵活运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
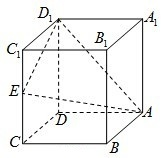 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )
如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )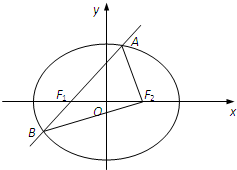 如图,椭圆E:
如图,椭圆E: