题目内容
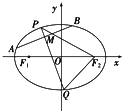 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求
| F2P |
| F2Q |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用椭圆C:
+
=1(a>b>0)的焦距为2,且过点(1,
),建立方程组,求出a,b,即可求椭圆C的方程;
(Ⅱ)分类讨论,求出直线PQ的方程,与椭圆方程联立,结合向量的数量积,M(-
,m)在椭圆的内部,利用换元法,即可求
•
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅱ)分类讨论,求出直线PQ的方程,与椭圆方程联立,结合向量的数量积,M(-
| 1 |
| 2 |
| F2P |
| F2Q |
解答:
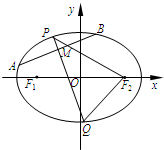 解:(Ⅰ)∵椭圆C:
解:(Ⅰ)∵椭圆C:
+
=1(a>b>0)的焦距为2,且过点(1,
),
∴
,
∴a2=2,b2=1…(2分)
∴椭圆C的方程为
+y2=1…(4分)
(Ⅱ)由题意,当直线AB垂直于x轴时,直线AB方程为x=-
,此时P(-
,0)、Q(
,0),
得
•
=(-
-1,0)•(
-1,0)=1-2=-1.…(5分)
当直线AB不垂直于x轴时,设直线AB的斜率为k(k≠0),M(-
,m),A(x1,y1),B(x2,y2)
由线段AB的中点M的横坐标为-
,得(x1+x2)+2(y1+y2)•
=0,则-1+4mk=0,
故4mk=1. …(6分)
此时,直线PQ斜率为k1=-4m,PQ的直线方程为y-m=-4m(x+
).
即y=-4mx-m.
联立
消去y,整理得(32m2+1)x2+16m2x+2m2-2=0.
设P(x3,y3),Q(x4,y4)
∴x3+x4=-
,x3x4=
. …(9分)
于是
•
=(x3-1)(x4-1)+y3y4=x3x4-(x3+x4)+1+(4mx3+m)(4mx4+m)
=(4m2-1)(x3+x4)+(16m2+1)x3x4+m2+1=
+
+1+m2
=
.…(11分)
由于M(-
,m)在椭圆的内部,故0<m2<
令t=32m2+1,1<t<29,则
•
=
-
. …(12分)
又1<t<29,所以-1<
•
<
.
综上,
•
的取值范围为(-1,
). …(13分)
 解:(Ⅰ)∵椭圆C:
解:(Ⅰ)∵椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
∴
|
∴a2=2,b2=1…(2分)
∴椭圆C的方程为
| x2 |
| 2 |
(Ⅱ)由题意,当直线AB垂直于x轴时,直线AB方程为x=-
| 1 |
| 2 |
| 2 |
| 2 |
得
| F2P |
| F2Q |
| 2 |
| 2 |
当直线AB不垂直于x轴时,设直线AB的斜率为k(k≠0),M(-
| 1 |
| 2 |
由线段AB的中点M的横坐标为-
| 1 |
| 2 |
| y1-y2 |
| x1-x2 |
故4mk=1. …(6分)
此时,直线PQ斜率为k1=-4m,PQ的直线方程为y-m=-4m(x+
| 1 |
| 2 |
即y=-4mx-m.
联立
|
设P(x3,y3),Q(x4,y4)
∴x3+x4=-
| 16m2 |
| 32m2+1 |
| 2m2-2 |
| 32m2+1 |
于是
| F2P |
| F2Q |
=(4m2-1)(x3+x4)+(16m2+1)x3x4+m2+1=
| (1+16m2)(2m2-2) |
| 32m2+1 |
| (4m2-1)(-16m2) |
| 32m2+1 |
=
| 19m2-1 |
| 32m2+1 |
由于M(-
| 1 |
| 2 |
| 7 |
| 8 |
令t=32m2+1,1<t<29,则
| F2P |
| F2Q |
| 19 |
| 32 |
| 51 |
| 32t |
又1<t<29,所以-1<
| F2P |
| F2Q |
| 125 |
| 232 |
综上,
| F2P |
| F2Q |
| 125 |
| 232 |
点评:本题考查椭圆的标准方程与几何性质,考查直线与椭圆的位置关系,考查向量知识的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
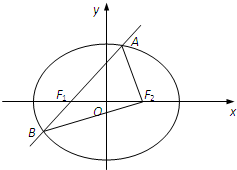 如图,椭圆E:
如图,椭圆E: