题目内容
对于函数f(x)=a-
(a∈R),
(Ⅰ)用单调性的定义证明函数f(x)的单调性;
(Ⅱ)是否存在实数a使函数f(x)为奇函数,若存在,请说明理由?
| 2 |
| 2x+1 |
(Ⅰ)用单调性的定义证明函数f(x)的单调性;
(Ⅱ)是否存在实数a使函数f(x)为奇函数,若存在,请说明理由?
考点:函数奇偶性的判断,函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:(Ⅰ)运用单调性的定义,即可判断,注意作差、变形,判断符号;
(Ⅱ)假设存在实数a使函数f(x)为奇函数,则f(0)=0,即可得到a.注意检验.
(Ⅱ)假设存在实数a使函数f(x)为奇函数,则f(0)=0,即可得到a.注意检验.
解答:
解:(Ⅰ)函数f(x)在R上递增.
理由如下:令m<n,则f(m)-f(n)=(a-
)-(a-
)
=
-
=
,
由于m<n,则2m<2n,
则f(m)-f(n)<0,即有函数f(x)在R上递增.
(Ⅱ)假设存在实数a使函数f(x)为奇函数,
则f(0)=0,即a-1═0,即a=1.
则函数f(x)=1-
=
,
f(-x)+f(x)=
+
=0,
故函数f(x)为奇函数.
理由如下:令m<n,则f(m)-f(n)=(a-
| 1 |
| 2m+1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2n+1 |
| 1 |
| 2m+1 |
| 2m-2n |
| (2m+1)(2n+1) |
由于m<n,则2m<2n,
则f(m)-f(n)<0,即有函数f(x)在R上递增.
(Ⅱ)假设存在实数a使函数f(x)为奇函数,
则f(0)=0,即a-1═0,即a=1.
则函数f(x)=1-
| 2 |
| 2x+1 |
| 2x-1 |
| 2x+1 |
f(-x)+f(x)=
| 2-x-1 |
| 2-x+1 |
| 2x-1 |
| 2x+1 |
故函数f(x)为奇函数.
点评:本题考查函数的性质和运用,考查函数的单调性的判断和函数的奇偶性的判断,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=cos4x-2sinxcosx-sin4x,则f(x)的最大值为( )
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
设an=-3n2+15n-18,则数列{an}中的最大项的值是( )
A、
| ||
B、
| ||
| C、0 | ||
| D、5 |
已知全集∪={1,2,3,4,5,6},集合A={1,3,4,5},B={5,6},则∁U(A∪B)=( )
| A、{1,3,4} |
| B、{5,6} |
| C、{1,3,4,5,6} |
| D、{2} |
已知集合A={x|x2-3x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A、[-2,-1] |
| B、[-1,-1] |
| C、[-1,2) |
| D、[1,2) |
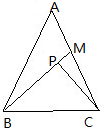 如图,在△ABC中,AB=AC=3
如图,在△ABC中,AB=AC=3