题目内容
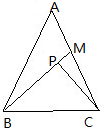如图，在△ABC中，AB=AC=3| 5 |
考点：向量在几何中的应用
专题：平面向量及应用
分析：以B为原点，建立平面直角坐标系，求出各点的坐标，得到
=（4，4），假设?P（x，y）在线段BM上使得PC⊥BM，
=（x-6，y），得方程组解出即可．
| BM |
| CP |
解答：
解：以B为原点，建立平面直角坐标系，
作AD⊥BC，垂足为D，
如图示：
∴易得A（3，6），M（4，4），C（6，0），
∴
=（4，4），
假设?P（x，y）在线段BM上使得PC⊥BM，
∴
=（x-6，y），
∴
，解得：x=y=3，
∴存在P在BM上，使得CP⊥BM，
P为边BM上靠近M点的一个四等分点．
解：以B为原点，建立平面直角坐标系，作AD⊥BC，垂足为D，
如图示：
∴易得A（3，6），M（4，4），C（6，0），
∴
| BM |
假设?P（x，y）在线段BM上使得PC⊥BM，
∴
| CP |
∴
|
∴存在P在BM上，使得CP⊥BM，
P为边BM上靠近M点的一个四等分点．
点评：本题考查了等腰三角形性质，考查了向量的应用，考查了两直线垂直的关于向量坐标的性质，是一道中档题．
练习册系列答案
相关题目
已知f（x）是定义在R上的函数，且满足f（1）=5，对任意实数x都有f′（x）＜3，则不等式f（x）＜3x+2的解集为（ ）
| A、（-∞，0） |
| B、（0，+∞） |
| C、（-∞，1） |
| D、（1，+∞） |
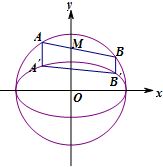如图，设AB、A′B′分别是圆O：x2+y2=4和椭圆C：