题目内容
5.已知双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的左、右焦点分别为F1,F2,焦距为2c,直线$y=\frac{{\sqrt{3}}}{3}(x+c)$与双曲线的一个交点P满足∠PF2F1=2∠PF1F2,则双曲线的离心率e为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}+1$ | D. | $\sqrt{3}+1$ |
分析 由题意∠F1PF2=90°,利用直角三角形的边角关系即可得到|PF2|=c,|PF1|=$\sqrt{3}$c,再利用双曲线的定义及离心率的计算公式即可得出.
解答 解:如图所示, ∠PF2F1=2∠PF1F2=60°,∠F1PF2=90°,
∠PF2F1=2∠PF1F2=60°,∠F1PF2=90°,
∴|PF2|=c,|PF1|=$\sqrt{3}$c,
由双曲线的定义可得:|PF1|-|PF2|=2a,
∴$\sqrt{3}c-c=2a$,
解得e=$\frac{c}{a}$=$\sqrt{3}+1$.
故选:D.
点评 熟练掌握圆的性质、直角三角形的边角关系、双曲线的定义、离心率的计算公式是解题的关键.

练习册系列答案
相关题目
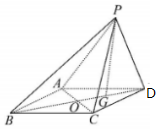 四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.
四棱锥P-ABCD中,四边形ABCD为平行四边形,AC与BD交于点O,点G为BD上一点,BG=2GD,$\overrightarrow{PA}$=$\overrightarrow{a}$,$\overrightarrow{PB}$=$\overrightarrow{b}$,$\overrightarrow{PC}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{PG}$=$\frac{2}{3}\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+\frac{2}{3}\overrightarrow{c}$.