题目内容
13．已知定义在R上的函数f（x）的图象关于原点对称，当x＞0时，有f（x）=2x-log3（x2-3x+5），则f（-2）=-3．分析 由题意，定义在R上的函数f（x）的图象关于原点对称，可知函数是奇函数，求出当x＜0时的解析式，可得答案．
解答 解：由题意，定义在R上的函数f（x）的图象关于原点对称，可知函数是奇函数，f（-x）=-f（x）．
当x＞0时，有f（x）=2x-log3（x2-3x+5），
当x＜0时，则-x＞0，有f（-x）=2-x-log3（x2+3x+5）=-f（x）．
∴当x＜0时，有f（x）=-2-x+log3（x2+3x+5），
则f（-2）=-22+log3（22-3×2+5）=-4+1=-3
故答案为：-3．
点评 本题考查了函数解析式的求法即带值计算问题，利用函数是奇函数这性质．属于基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
4．下列判断错误的是（ ）
| A． | “am2＜bm2”是“a＜b”的充分不必要条件 | |
| B． | 命题“?x∈R，x2-x-1≤0”的否定是“$?{x_0}∈{R}，{x_0}^2-{x_0}-1＞0$” | |
| C． | 若p，q均为假命题，则p∧q为假命题 | |
| D． | 若ζ～B（4，0.25），则Dξ=1 |
5．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1，F2，焦距为2c，直线$y=\frac{{\sqrt{3}}}{3}（x+c）$与双曲线的一个交点P满足∠PF2F1=2∠PF1F2，则双曲线的离心率e为（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $2\sqrt{3}+1$ | D． | $\sqrt{3}+1$ |
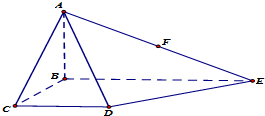如图，在四棱锥A-BCDE中，底面BCDE是∠BCD=90°的梯形，CD∥BE，AB⊥底面BCDE，BE=4AB=2BC=2CD，点F为AE的中点．