题目内容
15.已知等比数列{an}的各项均为正数,Sn为其前n项和,对于任意的n∈N*,满足关系式2Sn=3an-3.(1)求数列{an}的通项公式;
(2)设数列{bn}的通项公式是bn=$\frac{1}{lo{g}_{3}{a}_{n}(lo{g}_{3}{{a}_{n}}^{2}+1)}$,求证对一切的正整数n都有:b1+b2+…+bn<$\frac{2}{3}$.
分析 (1)当n≥2时,有2Sn-1=3an-1-3,2Sn=3an-3,两式相减,得an=3an-1(n≥2),由此能求出an=3n.
(2)把{an}的通项公式代入bn=$\frac{1}{lo{g}_{3}{a}_{n}(lo{g}_{3}{{a}_{n}}^{2}+1)}$,得当n≥2时,$\frac{1}{n(2n+1)}=\frac{2}{2n(2n+1)}<\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}-\frac{1}{2n+1}$,即可.
解答 解:(1)当n≥2时,有2Sn-1=3an-1-3,①
又2Sn=3an-3,②
②-①得,2(Sn-Sn-1)=2an=3an-3an-1,
即an=3an-1(n≥2).
又当n=1时,2a1=3a1-3,
∴a1=3.
故数列{an}为等比数列,且公比q=3.
∴an=3n.
数列{an}的通项公式an=3n;
(2)证明:∵log3an=n,∴bn=$\frac{1}{lo{g}_{3}{a}_{n}(lo{g}_{3}{{a}_{n}}^{2}+1)}$=$\frac{1}{n(2n+1)}$
当n≥2时,$\frac{1}{n(2n+1)}=\frac{2}{2n(2n+1)}<\frac{2}{(2n-1)(2n+1)}$=$\frac{1}{2n-1}-\frac{1}{2n+1}$,${b}_{1}=\frac{1}{3}$
正整数n都有:b1+b2+…+bn<b1$+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1}=\frac{2}{3}-\frac{1}{2n+1}$+$\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1}$
=$\frac{2}{3}$-$\frac{1}{2n+1}$<$\frac{2}{3}$.
点评 本题考查了 递推式的应用及简单的放缩再“裂项求和”求数列的前n项和,考查了推理能力与计算能力,属于中档题.

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}+1$ | D. | $\sqrt{3}+1$ |
| A. | c>b>a | B. | b>c>a | C. | c>a>b | D. | a>b>c |
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
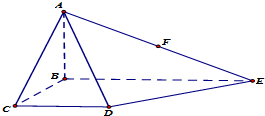 如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.
如图,在四棱锥A-BCDE中,底面BCDE是∠BCD=90°的梯形,CD∥BE,AB⊥底面BCDE,BE=4AB=2BC=2CD,点F为AE的中点.