题目内容
已知锐角△ABC中,AD是高,O是外心,AO的延长线交过O、B、C三点的圆于P,自P作PE⊥AB于E,PF⊥AC于F.求证:DEPF是平行四边形.
考点:向量在几何中的应用,平行向量与共线向量
专题:证明题
分析:先证△ADC∽△AEP,从而可得△ADC∽△ACP,则DE:CP=AD:AC=sin∠ACD,又∠PCF=∠ACD,则sin∠PCF=sin∠ACD=PF:CP,所以DE:CP=PF:CP,则DE=PF,同理可证,DF=PE,从而可证得.
解答:
证明:如图所示,∵∠DAC是∠ACD的余角,
又∠BOA=2∠ACD,O是外心,
∴∠BAO也与∠ACD互余,
∴∠DAC=∠BAO,又∠ADC=∠AEP,
所以△ADC∽△AEP,∴AD:AE=AC:AP,
∴△ADC∽△ACP,
∴DE:CP=AD:AC=sin∠ACD,
又∠PCF=∠ACD,∴sin∠PCF=sin∠ACD=PF:CP,
∴DE:CP=PF:CP,∴DE=PF,同理可证,DF=PE,∴DEPF是平行四边形.
又∠BOA=2∠ACD,O是外心,

∴∠BAO也与∠ACD互余,
∴∠DAC=∠BAO,又∠ADC=∠AEP,
所以△ADC∽△AEP,∴AD:AE=AC:AP,
∴△ADC∽△ACP,
∴DE:CP=AD:AC=sin∠ACD,
又∠PCF=∠ACD,∴sin∠PCF=sin∠ACD=PF:CP,
∴DE:CP=PF:CP,∴DE=PF,同理可证,DF=PE,∴DEPF是平行四边形.
点评:本题主要考查了平面几何知识,以及三角形相似的应用,同时考查了学生分析问题和解决问题的能力,以及运算求解的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
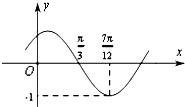 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 3 |
| A、f(x)=sin2x | ||
| B、f(x)=-sin2x | ||
C、f(x)=sin(2x-
| ||
D、f(x)=sin(2x+
|
函数f(x)=
(x∈R)的值域是( )
| x |
| x2+1 |
A、[-
| ||||
B、[0,
| ||||
C、(-
| ||||
D、[-
|
已知函数f(x)=ex-1,g(x)=-x2+4x-4,若存在实数a使f(a)=g(b),则b的取值范围为( )
| A、[1,+∞) | ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
| 3 |
| π |
| 12 |
| π |
| 12 |
| A、0 | ||
B、-
| ||
C、
| ||
| D、2 |