题目内容
| 3 |
| π |
| 12 |
| π |
| 12 |
| A、0 | ||
B、-
| ||
C、
| ||
| D、2 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：变形可得原式=2（sin
cos
-cos
sin
），由两角差的正弦函数可得．
| π |
| 3 |
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
解答：
解：
cos
-sin
=2（
cos
-
sin
）
=2（sin
cos
-cos
sin
）
=2sin（
-
）=2sin
=
故选：C
| 3 |
| π |
| 12 |
| π |
| 12 |
| ||
| 2 |
| π |
| 12 |
| 1 |
| 2 |
| π |
| 12 |
=2（sin
| π |
| 3 |
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
=2sin（
| π |
| 3 |
| π |
| 12 |
| π |
| 4 |
| 2 |
故选：C
点评：本题考查两角和与差的正弦函数，属基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
相关题目
双曲线
-
=1（b＞0）的焦距为6，则双曲线的渐近线方程为（ ）
| x2 |
| 4 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|
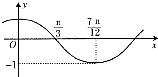
函数的图象如图所示，为了得到的图象，则只要将f（x）=cos2x的函数的图象（ ）
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知x+x-1=3，则x3+x-3=（ ）
A、8
| ||
B、3
| ||
| C、18 | ||
D、±
|
下列函数中，满足“?x1，x2∈（0，+∞）且x1≠x2，有（x1-x2）[f（x1）-f（x2）]＜0”的是（ ）
| A、f（x）=2x | ||
| B、f（x）=-（x-1）2 | ||
C、f（x）=
| ||
| D、f（x）=ln（x+1） |
某质点在25S内运动速度V是时间t的函数，它的图象如图所示，用解析法表示出这个函数，并求出6S时质点的速度．