题目内容
若△ABC的内角A、B、C的对边分别是a，b，c，且asinA+csinC-bsinB=
asinC，则cosB等于 ．
| 2 |
考点：正弦定理,余弦定理
专题：解三角形
分析：由条件利用正弦定理求得 a2+c2-b2=
ac，再利用余弦定理求得cosB的值．
| 2 |
解答：
解：△ABC中，∵asinA+csinC-bsinB=
asinC，则由正弦定理可得 a2+c2-b2=
ac，
∴由余弦定理可得cosB=
=
，
故答案为：
．
| 2 |
| 2 |
∴由余弦定理可得cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 2 |
故答案为：
| ||
| 2 |
点评：本题主要考查正弦定理和余弦定理的应用，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数的图象如图所示，为了得到的图象，则只要将f（x）=cos2x的函数的图象（ ）
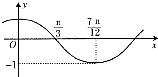
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
下列函数中，满足“?x1，x2∈（0，+∞）且x1≠x2，有（x1-x2）[f（x1）-f（x2）]＜0”的是（ ）
| A、f（x）=2x | ||
| B、f（x）=-（x-1）2 | ||
C、f（x）=
| ||
| D、f（x）=ln（x+1） |