Question

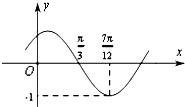函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示，将f（x）的图象向左平移

π

3

个长度单位，所得图象对应的函数解析式为（　　）

• A、f（x）=sin2x
• B、f（x）=-sin2x
• C、f（x）=sin（2x-

  2π

  3

  ）
• D、f（x）=sin（2x+

  2π

  3

  ）

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：计算题,三角函数的图像与性质

分析：依题意，知A=1，T=π，从而可求ω=2；再由

π

3

ω+φ=2kπ+π（k∈Z），|φ|＜

π

2

可求得φ，从而可得y=f（x）的解析式，最后利用函数y=Asin（ωx+φ）的图象变换即可求得将f（x）的图象向左边平移

π

3

 个长度单位所得图象对应的函数解析式．

解答： 解：依题意，知A=1，

1

4

T=

7π

12

-

π

3

=

π

4

，
∴T=

2π

ω

=π，ω=2；又

π

3

ω+φ=2kπ+π（k∈Z），
∴φ=2kπ+

π

3

（k∈Z），又|φ|＜

π

2

，
∴φ=

π

3

，
∴f（x）=sin（2x+

π

3

），
∴将f（x）的图象向左边平移

π

3

个长度单位，
得y=f（x+

π

3

）=sin[2（x+

π

3

）+

π

3

]=sin（2x+π）=-sin2x，
故选：B．

点评：本题考查函数y=Asin（ωx+φ）的图象的解析式的确定及图象变换，考查分析运算能力，属于中档题．