题目内容
已知sinα=
，α∈（
，π），则cosα的值为（ ）
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：首先根据α所在的象限，利用已知条件求得cosα值的符号，然后根据sin2α+cos2α=1进一步求出cosα的值．
解答：
解：已知α∈（
，π），则α的中终边在第二象限内．
已知sinα=
根据三角恒等式sin2α+cos2α=1
进一步求出cosα=-
，
故选：D．
| π |
| 2 |
已知sinα=
| 3 |
| 5 |
进一步求出cosα=-
| 4 |
| 5 |
故选：D．
点评：本题考查的知识点：三角恒等式，根据已知α所在的象限角确定三角函数的符号．
练习册系列答案
全能闯关100分系列答案
相关题目
在函数y=tanx、y=|sinx|、y=cos（2x+
）中，最小正周期为π的函数的个数为（ ）
| 2π |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
有不同的语文书9本，不同的数学书7本，不同的英语书5本，从中选出不属于同一学科的书2本，则不同的选法有（ ）种．
| A、21 | B、315 |
| C、143 | D、153 |
log
27的值是（ ）
| 3 |
| A、3 | B、-3 | C、6 | D、-6 |
在△ABC中，根据下列条件解三角形，其中有两个解的是（ ）
| A、b=10，A=45°，C=70° |
| B、a=60，A=45°，B=60° |
| C、a=7，b=5，A=80° |
| D、b=14，b=16，C=45° |
直线l的倾斜角为α，sinα=
，若P（4，2）在直线l上，则直线l的方程（ ）
| ||
| 2 |
| A、x-y-2=0，或x+y-6=0 | ||||
| B、x-y-1=0，或x+y-3=0 | ||||
| C、x+y-2=0，或x-y-6=0 | ||||
D、
|
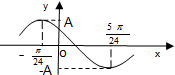已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-