题目内容
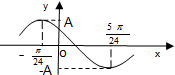已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），其部分图象如图所示，且直线y=A与曲线y=f（x）（-| π |
| 24 |
| 11π |
| 24 |
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| 2013π |
| 8 |
| 2013 |
 |
| i=1 |
| i•π |
| 8 |
| A、1 | B、-1 | C、0 | D、2 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,定积分在求面积中的应用
专题：三角函数的图像与性质
分析：由周期求出ω，由五点法作图求出φ的值，再根据直线y=A与曲线y=f（x）（-
≤x≤
）所围成的封闭图形的面积为π求出A，可得函数的解析式．再利用函数的周期性求出所给式子的值．
| π |
| 24 |
| 11π |
| 24 |
解答：
解：由函数的图象可得
•
=
+
，求得ω=4，可得函数的周期为
．
再根据五点法作图可得4×（-
）+φ=
，求得φ=
．
区间[-
，
]的长度恰好为函数的一个周期，直线y=A与曲线y=f（x）（-
≤x≤
）所围成的封闭图形的面积为
（2A×
）=π，
∴A=2，函数f（x）=2sin（4x+
）．
在一个周期[1，
]上，f（
）=2cos
=-1，f（
）=-2sin
=-
，+f（
）=-2cos
=1，f（
）=
，
∴f（
）+f（
）+f（
）+f（
）=0．
∴f（
）+f（
）+f（
）+…+f（
）=503[f（
）+f（
）+f（
）+f（
）]+f（
）=0+1=1，
故选：B．
| 1 |
| 2 |
| 2π |
| ω |
| 5π |
| 24 |
| π |
| 24 |
| π |
| 2 |
再根据五点法作图可得4×（-
| π |
| 24 |
| π |
| 2 |
| 2π |
| 3 |
区间[-
| π |
| 24 |
| 11π |
| 24 |
| π |
| 24 |
| 11π |
| 24 |
| 1 |
| 2 |
| π |
| 2 |
∴A=2，函数f（x）=2sin（4x+
| 2π |
| 3 |
在一个周期[1，
| π |
| 2 |
| π |
| 8 |
| 2π |
| 3 |
| 2π |
| 8 |
| 2π |
| 3 |
| 3 |
| 3π |
| 8 |
| 2π |
| 3 |
| π |
| 2 |
| 3 |
∴f（
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
∴f（
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| 2013π |
| 8 |
| π |
| 8 |
| 2π |
| 8 |
| 3π |
| 8 |
| π |
| 2 |
| π |
| 8 |
故选：B．
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，利用函数的周期性求函数的值，属于基础题．
练习册系列答案
相关题目
已知集合M={2，log2a}，N={a，b}，若M∩N={0}，则M∪N=（ ）
| A、{0，1} |
| B、{0，1，2} |
| C、{1，2} |
| D、{0，2} |
已知|
|=5，|
|=1．若
=λ
且
与
的方向相反，则λ=（ ）
| a |
| b |
| a |
| b |
| b |
| a |
| A、5 | ||
| B、-5 | ||
C、
| ||
D、-
|
已知sinα=
，α∈（
，π），则cosα的值为（ ）
| 3 |
| 5 |
| π |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
某程序框图如图所示，则该程序运行后输出的S的值为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
设曲线y=x2在点（a，a2）处的切线与直线x+2y+a=0垂直，则a的值为（ ）
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
若lna＜0，(
)b＞1，则（ ）
| 1 |
| 3 |
| A、a＞1，b＞0 |
| B、0＜a＜1，b＞0 |
| C、a＞1，b＜0 |
| D、0＜a＜1，b＜0 |