题目内容
6.已知点A、B、C、D在同一球面上,AB=3,BC=4,AC=5,若四面体ABCD体积的最大值为10,则这个球的表面积为( )| A. | $\frac{25π}{4}$ | B. | $\frac{125π}{4}$ | C. | $\frac{225π}{16}$ | D. | $\frac{625π}{16}$ |
分析 根据几何体的特征,判定外接球的球心,求出球的半径,即可求出球的表面积.
解答  解:根据题意知,△ABC是一个直角三角形,其面积为6.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,
解:根据题意知,△ABC是一个直角三角形,其面积为6.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,
若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,
所以,DQ与面ABC垂直时体积最大,最大值为$\frac{1}{3}$×S△ABC×DQ=10,
即$\frac{1}{3}$×6×DQ=10,∴DQ=5,如图.
设球心为O,半径为R,则在直角△AQO中,
OA2=AQ2+OQ2,即R2=2.52+(5-R)2,∴R=$\frac{25}{8}$,
则这个球的表面积为:S=4π($\frac{25}{8}$)2=$\frac{625π}{16}$.
故选:D.
点评 本题考查的知识点是球内接多面体,球的表面积,其中分析出何时四面体ABCD的体积的最大值,是解答的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
16.已知集合A={x|0<x<3},B=$\left\{{x|y=\sqrt{{x^2}-1}}\right\}$,则集合A∩(∁RB)为( )
| A. | [0,1) | B. | (0,1) | C. | [1,3) | D. | (1,3) |
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )
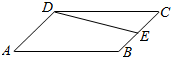

| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |
14.设函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥0}\\{f(-x),x<0}\end{array}\right.$,则f(log2$\frac{1}{6}$)=( )
| A. | -$\frac{1}{6}$ | B. | -6 | C. | 6 | D. | $\frac{1}{6}$ |
18.若m>n,则( )
| A. | 0.2m<0.2n | B. | log0.3m>log0.3n | C. | 2m<2n | D. | m2>n2 |



