题目内容
1.已知圆C的方程为x2+y2=4,点M(t,3),若圆C上存在两点A,B满足$\overrightarrow{MA}=\overrightarrow{AB}$,则t的取值范围是$[{-3\sqrt{3},3\sqrt{3}}]$.分析 由向量等式可得,A是MB的中点,利用圆x2+y2=4的直径是4,可得MA≤4,即点M到原点距离小于等于6,由此列式可得t的取值范围.
解答 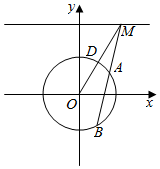 解:如图,连结OM交圆于点D.
解:如图,连结OM交圆于点D.
∵$\overrightarrow{MA}=\overrightarrow{AB}$,∴A是MB的中点,
∵圆x2+y2=4的直径是4,
∴MA=AB≤4,
又∵MD≤MA,OD=2,
∴OM≤6,
即点M到原点距离小于等于6,
∴t2+9≤36,
∴-$3\sqrt{3}$≤t≤$3\sqrt{3}$,
故答案为:$[{-3\sqrt{3},3\sqrt{3}}]$.
点评 本题考查向量知识的运用,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
12.下列函数中,既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=lnx | B. | y=x3 | C. | y=x2 | D. | y=sinx |
16.设集合A={-1,0,1},B={x|lgx≤0},则A∩B=( )
| A. | {-1,0,1} | B. | {1} | C. | {-1} | D. | {-1,1} |
6.已知点A、B、C、D在同一球面上,AB=3,BC=4,AC=5,若四面体ABCD体积的最大值为10,则这个球的表面积为( )
| A. | $\frac{25π}{4}$ | B. | $\frac{125π}{4}$ | C. | $\frac{225π}{16}$ | D. | $\frac{625π}{16}$ |
