题目内容
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )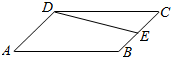
| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |
分析 利用平面向量的三角形法则用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{DE}$.
解答 解:∵四边形ABCD是平行四边形,∴$\overrightarrow{AB}=\overrightarrow{DC}$,$\overrightarrow{AD}=\overrightarrow{BC}$,
∵E是BC中点,∴$\overrightarrow{CE}$=-$\frac{1}{2}$$\overrightarrow{BC}$=-$\frac{1}{2}$$\overrightarrow{AD}$.
∴$\overrightarrow{DE}$=$\overrightarrow{DC}+\overrightarrow{CE}$=$\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AD}$.∴x=1,y=-$\frac{1}{2}$.
故选D:.
点评 本题考查了平面向量的线性运算法则,平面向量的基本定理,属于基础题.

练习册系列答案
相关题目
7.已知定义在R上的奇函数f (x)满足f(x)=f(4-x),且在区间[0,2]上是增函数,那么( )
| A. | f(6)<f(4)<f(1) | B. | f(4)<f(6)<f(1) | C. | f(1)<f(6)<f(4) | D. | f(6)<f(1)<f(4) |
12.下列函数中,既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=lnx | B. | y=x3 | C. | y=x2 | D. | y=sinx |
2.已知点$(a,\frac{1}{2})$在幂函数f(x)=(a-1)xb的图象上,则函数f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 定义域内的减函数 | D. | 定义域内的增函数 |
6.已知点A、B、C、D在同一球面上,AB=3,BC=4,AC=5,若四面体ABCD体积的最大值为10,则这个球的表面积为( )
| A. | $\frac{25π}{4}$ | B. | $\frac{125π}{4}$ | C. | $\frac{225π}{16}$ | D. | $\frac{625π}{16}$ |