题目内容
15.一个袋中装有7个大小相同的球,其中红球有4个,编号分别为1,2,3,4;蓝球3个,编号为2,4,6,现从袋中任取3个球(假设取到任一球的可能性相同).(I)求取出的3个球中,含有编号为2的球的概率;
(Ⅱ)记ξ为取到的球中红球的个数,求ξ的分布列和数学期望.
分析 (I)从7个球中取出3个球,基本事件总数n=C73=35,然后求出取出的3个球中,含有编号为2的球的结果数,代入古典概率的求解公式即可求解
(II)先判断随机变量ξ所有可能取值为0,1,2,3,根据题意求出随机变量的各个取值的概率,即可求解分布列及期望值.
解答 解:(Ⅰ) 设“取出的3个球中,含有编号为2的球”为事件A,则
从盒子中取出3个球,基本事件总数n=C73=35,
其中含有2号球的基本事件个数m=C21C52+C22C51=25,
∴取出的3个球中,含有编号为2的球的概率$\frac{25}{35}$=$\frac{5}{7}$.…(5分)
(Ⅱ)ξ所有可能取值为0,1,2,3.…(6分)
P(ξ=0)=$\frac{1}{35}$,P(ξ=1)=$\frac{4{C}_{3}^{2}}{35}$=$\frac{12}{35}$,P(ξ=2)=$\frac{{C}_{4}^{2}{C}_{3}^{1}}{35}$=$\frac{18}{35}$,P(ξ=3)=$\frac{{C}_{4}^{3}}{35}$=$\frac{4}{35}$,…(10分)
所以随机变量ξ的分布列是
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{35}$ | $\frac{12}{35}$ | $\frac{18}{35}$ | $\frac{4}{35}$ |
点评 本题主要考查了古典概型及计算公式,互斥事件、离散型随机变量的分布列及期望值的求解,考查了运用概率知识解决实际问题的能力.

练习册系列答案
相关题目
6.已知点A、B、C、D在同一球面上,AB=3,BC=4,AC=5,若四面体ABCD体积的最大值为10,则这个球的表面积为( )
| A. | $\frac{25π}{4}$ | B. | $\frac{125π}{4}$ | C. | $\frac{225π}{16}$ | D. | $\frac{625π}{16}$ |
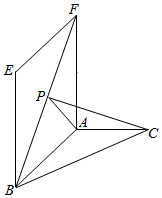 如图所示,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.
如图所示,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2$\sqrt{3}$,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.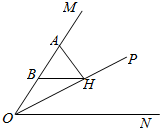 如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.
如图,OP平分∠MON,AH⊥OP于H,B是AO的中点,求证:BH∥ON.