题目内容
16．若函数f（x）满足对任意实数x∈R都有f（x+1）=-f（x），试判断f（x）是否为周期函数．分析 把x+2拆成1+（x+1），代入f（1+x）=-f（x），再利用函数的周期性定义证明即可．
解答 解：对任意实数x都有
f（x+2）=f[1+（1+x）]=-f（1+x）=f（x），
∴f（x+2）=f（x）
∴函数f（x）是以2为周期的周期函数．
点评 本题主要考查函数的周期性的定义的应用，属于基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
6．已知点A、B、C、D在同一球面上，AB=3，BC=4，AC=5，若四面体ABCD体积的最大值为10，则这个球的表面积为（ ）
| A． | $\frac{25π}{4}$ | B． | $\frac{125π}{4}$ | C． | $\frac{225π}{16}$ | D． | $\frac{625π}{16}$ |
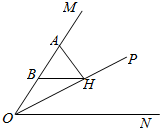如图，OP平分∠MON，AH⊥OP于H，B是AO的中点，求证：BH∥ON．