题目内容
函数f（x）=x2+（k+1）x+7有一根在[1，2]时，求k的取值范围．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：本题可根据有一根在[1，2]进行分类，分为方程有且只有一根在[1，2]内和有两根均在[1，2]内，得到k满足的关系式，化简得到本题结果．
解答：
解：∵f（x）=x2+（k+1）x+7有一根在[1，2]内，
∴f（1）f（2）≤0或
，
解之得：-9≤k≤-
．
∴-9≤k≤-
．
∴f（1）f（2）≤0或
|
解之得：-9≤k≤-
| 13 |
| 2 |
∴-9≤k≤-
| 13 |
| 2 |
点评：本题考查的是方程根的分布，还考查了二次函数的图象和分类讨论的数学思想，本题有一难度，属于中档题．
练习册系列答案
相关题目
数列{an}中，a2=2，a6=0且数列{
}是等差数列，则a8=（ ）
| 1 |
| an+1 |
A、
| ||
B、
| ||
C、-
| ||
D、
|
已知函数f（x）=-x3+bx2-
b3（b＞0），有且仅有两个不同的零点x1，x2，则（ ）
| 4 |
| 27 |
| A、x1+x2＞0，x1x2＜0 |
| B、x1+x2＞0，x1x2＞0 |
| C、x1+x2＜0，x1x2＜0 |
| D、x1+x2＜0，x1x2＞0 |
已知定义域为R的函数f （x）满足对任意的x1，x2∈（8，+∞）（x1＜x2），有f（x1）＞f（x2），且函数y=f（x+8）为偶函数，则（ ）
| A、f （6）＞f （7） |
| B、f （6）＞f （9） |
| C、f （7）＞f （9） |
| D、f （7）＞f （10） |
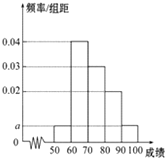某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]