题目内容
已知函数f(x)=alnx-ax-3(a∈R).
(1)当 a=-1时,证明:在(1,+∞)上,f(x)+2>0;
(2)求证:
•
•
…
<
(n≥2,n∈N+).
(1)当 a=-1时,证明:在(1,+∞)上,f(x)+2>0;
(2)求证:
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln4 |
| 4 |
| lnn |
| n |
| 1 |
| n |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用导数求得函数在(1,+∞)上的最小值为f(1)=-2,即可得出证明;
(2)由(1)得-ln x+x-3+2>0,即ln x<x-1对一切x∈(1,+∞)恒成立.0<ln n<n-1,即0<
<
,即可得出结论成立.
(2)由(1)得-ln x+x-3+2>0,即ln x<x-1对一切x∈(1,+∞)恒成立.0<ln n<n-1,即0<
| lnn |
| n |
| n-1 |
| n |
解答:
解:(1)根据题意知,f′(x)=
(x>0),
当a>0时,f(x)的单调递增区间为(0,1],单调递减区间为(1,+∞);
当a<0时,f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1];
当a=0时,f(x)不是单调函数.
所以a=-1时,f(x)=-ln x+x-3,在(1,+∞)上单调递增,
所以f(x)>f(1),
即f(x)>-2,所以f(x)+2>0.…(6分)
(2)由(1)得-ln x+x-3+2>0,即-ln x+x-1>0,
所以ln x<x-1对一切x∈(1,+∞)恒成立.∵n≥2,n∈N*,
则有0<lnn<n-1,∴0<
<
,
∴
•
•
•…•
<
•
•
•…•
=
(n≥2,n∈N*). …(12分)
| a(1-x) |
| x |
当a>0时,f(x)的单调递增区间为(0,1],单调递减区间为(1,+∞);
当a<0时,f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1];
当a=0时,f(x)不是单调函数.
所以a=-1时,f(x)=-ln x+x-3,在(1,+∞)上单调递增,
所以f(x)>f(1),
即f(x)>-2,所以f(x)+2>0.…(6分)
(2)由(1)得-ln x+x-3+2>0,即-ln x+x-1>0,
所以ln x<x-1对一切x∈(1,+∞)恒成立.∵n≥2,n∈N*,
则有0<lnn<n-1,∴0<
| lnn |
| n |
| n-1 |
| n |
∴
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln4 |
| 4 |
| lnn |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n-1 |
| n |
| 1 |
| n |
点评:本题主要考查利用导数判断函数的单调性求函数的最值知识,考查利用导数证明不等式问题,注意构造函数法的应用,属于难题.

练习册系列答案
相关题目
椭圆
+
=1(a>b>0)的两个焦点是F1、F2,以|F1F2|为斜边作等腰直角三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
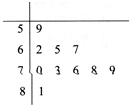 已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.
已知某单位由50名职工,将全体职工随机按1-50编号,并且按编号顺序平均分成10组,先要从中抽取10名职工,各组内抽取的编号依次增加5进行系统抽样.